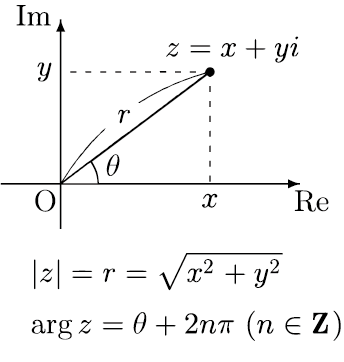第1講 複素数の表し方と演算
複素数
複素数とは，実数 $x$，$y$，および $i^2=-1$ を満たす特別な「数」$i$ を用いて
$x+yi$
と表される「数」のことである．
$i$ を
虚数単位，
$x$ をこの複素数の
実部，
$y$ をこの複素数の
虚部と呼ぶ．
複素数 $z$ の実部，虚部はそれぞれ $\mathrm{Re}z$，$\mathrm{Im}z$ と表すことが多い．
例えば
$\mathrm{Re}(2+3i)=2$，
$\mathrm{Im}(2+3i)=3$
表記法は基本的に実数の文字式と同じ規則に従う．
例えば
$2+(-3)i=2-3i$
$2+1i=2+i$
など．
また，$x+yi$ を $x+iy$ と書いても問題ないが，数字を後に，例えば $3i$ のことを $i3$ と書くのは好まれない．「$i\pi$」や「$ie$」はいいのに「$i3$」や「$i\sqrt{2}$」はよくないというのは理不尽といえば理不尽だが，あくまで習慣的なものであってどちらも禁止されているわけではない．
虚部が $0$ である複素数は実数ということになるが，実数でない複素数，すなわち虚部が $0$ でない複素数を
虚数と呼ぶ．また，実部が $0$ である虚数を
純虚数と呼ぶ．
$\mathrm{(1)}$ 複素数 $\mathrm{(2)}$ 実数 $\mathrm{(3)}$ 虚数 $\mathrm{(4)}$ 純虚数 であるものをそれぞれについて次からすべて選べ．
| $\mathrm{(a)}$ $0$ |
$\mathrm{(b)}$ $1+\sqrt{2}$ |
| $\mathrm{(c)}$ $-\sqrt{5}i\quad$ |
$\mathrm{(d)}$ $2-i$ |
$\mathrm{(1)}$ 複素数：$\mathrm{(a),(b),(c),(d)}$
$\mathrm{(2)}$ 実数；$\mathrm{(a),(b)}$
$\mathrm{(3)}$ 虚数：$\mathrm{(c),(d)}$
$\mathrm{(4)}$ 純虚数：$\mathrm{(c)}$
複素数の基本演算
- 複素数の加法・減法は実部，虚部それぞれについて行われる．
| $(4+3i)+(1+5i)$ | $=(4+1)+(3+5)i$ |
| $=5+8i$ |
| $(4+3i)-(1+5i)$ | $=(4-1)+(3-5)i$ |
| $=3-2i$ |
-
複素数の乗法は，分配法則を用いて「展開」し，$i^2$ が現れたら $-1$ で置き換えればよい．
| $(1+2i)(3+i)$ | $=3+7i+2i^2$ |
| $=3+7i-2$ |
| $=1+7i$ |
| $(3+4i)(3-4i)$ | $=9-16i^2$ |
| $=9+16$ |
| $=25$ |
-
複素数の除法は，無理数の「有理化」と同じ要領で分母の「実数化」を行えばよい．
| $\dfrac{1+2i}{2+i}$ | $=\dfrac{(1+2i)(2-i)}{(2+i)(2-i)}$ |
| $=\dfrac{2+3i-2i^2}{2^2-i^2}$ |
| $=\dfrac{4+3i}{5}$ $=\dfrac{4}{5}+\dfrac{3}{5}i$ |
本来であれば，複素数 $z_1=x_1+y_1i$，$z_2=x_2+y_2i$ の加減乗除を
$z_1+ z_2=(x_1+ x_2)+(y_1+ y_2)i$
$z_1- z_2=(x_1- x_2)+(y_1- y_2)i$
$z_1z_2=x_1x_2-y_1y_2+(x_1y_2+x_2y_1)i$
$\dfrac{z_1}{z_2}=\dfrac{x_1x_2+y_1y_2}{{x_2}^2+{y_2}^2}+\dfrac{-x_1y_2+x_2y_1}{{x_2}^2+{y_2}^2}i$
と定義した上で，これらの演算に関して結合法則・交換法則・分配法則が確かに成り立つことを証明する必要がある．もちろん地道にその作業をやってもよいのだが，おそらく最も見通しがよいのは，複素数 $x+yi$ を
$\left(\begin{array}{cc}x&-y\\y&x\end{array}\right)$
という行列とみなすことであろう．例えば積に関しては
$\left(\begin{array}{cc}x_1&-y_1\\y_1&x_1\end{array}\right)
\left(\begin{array}{cc}x_2&-y_2\\y_2&x_2\end{array}\right)
$$=\left(\begin{array}{cc}x_1x_2-y_1y_2&-(x_1y_2+x_2y_1)\\x_1y_2+x_2y_1&x_1x_2-y_1y_2\end{array}\right)$
が成り立ち，確かに複素数の演算と整合していることがわかる．
従って，行列の演算に関して結合法則・交換法則・分配法則が成り立つ(そちらは証明する必要があるが)ことから，複素数の演算に関してもこれらの法則が成り立つことが結論できるのである．
複素数 $z=x+yi$ の虚部の符号を変えて得られる複素数を $z$ の
複素共役と呼び，$\overline{z}$ で表す：
$\overline{z}=\overline{x+yi}=x-yi$
$\overline{1+2i}=1-2i$
$\overline{\sqrt{5}}=\sqrt{5}$
$\overline{-3i}=3i$
次を満たす複素数 $z$ はどのような数か？
$\mathrm{(1)}$ $\overline{z}=z$
$\mathrm{(2)}$ $\overline{z}=-z$
$\mathrm{(1)}$ 実数
$\mathrm{(2)}$ 純虚数または $0$
次が成り立つことを確かめるのは容易であろう：
$\overline{\overline{z}}=z$
$\overline{z+w}=\overline{z}+\overline{w}$
$\overline{zw}=\overline{z}\cdot\overline{w}$
$\overline{\Big(\dfrac{z}{w}\Big)}=\dfrac{\overline{z}}{\overline{w}}$ (ただし $w\neq0$)
複素平面，絶対値と偏角
複素数は二つの実数を用いて表されるのであるから，下の図のように
複素平面と呼ばれる平面上の点として表すこともできる．
すなわち、実部を横軸(
実軸)上に、虚部を縦軸(
虚軸)上にとり，複素数を平面上の点と見なすのである．
複素平面上において，複素数 $z$ の
絶対値 $|z|$ は 原点 $\mathrm{O}$ (あるいは複素数 $0$ )と $z$ とを結ぶ線分 $0z$ の長さであり，
偏角 $\arg{z}$ は $0z$ と実軸の正方向とのなす角である．ただし，偏角は指定のない限り一般角としてとるので一意ではない．
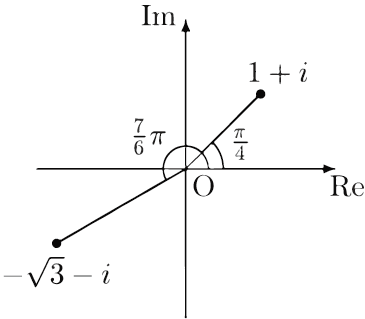
複素数 $1+i$ と $-\sqrt{3}-i$ を複素平面上に表すと次のようになる：
また，絶対値と偏角はそれぞれ次の通り：
$|1+i|=\sqrt{1^2+1^2}=\sqrt{2}$
$\arg(1+i)=\dfrac{\pi}{4}+2n\pi\ (n\in\mathbf{Z})$
$|-\sqrt{3}-i|=\sqrt{(-\sqrt{3})^2+(-1)^2}=2$
$\arg(-\sqrt{3}-i)=\dfrac{7}{6}\pi+2n\pi\ (n\in\mathbf{Z})$
偏角の表し方には任意性がある．例えば，$\arg(-\sqrt{3}-i)$ は
$\arg(-\sqrt{3}-i)=-\dfrac{5}{6}\pi+2n\pi\ (n\in\mathbf{Z})$
と表すこともできる．
絶対値と偏角の性質としては次が重要である：
$\mathrm{(a)}$ $|zw|=|z|\cdot|w|$
$\mathrm{(b)}$ $|z+w|\le |z|+|w|$
$\mathrm{(c)}$ $\bigg|\,\dfrac{z}{w}\,\bigg|=\dfrac{|z|}{|w|}$
$\mathrm{(d)}$ $|\overline{z}|=|z|$
$\mathrm{(e)}$ $z\overline{z}=|z|^2$
$\mathrm{(f)}$ $\arg{(zw)}=\arg{z}+\arg{w}$
$\mathrm{(g)}$ $\arg{\dfrac{z}{w}}=\arg{z}-\arg{w}$
$\mathrm{(h)}$ $\arg{\overline{z}}=-\arg{z}$
ただし，$\mathrm{(c)}$ では $w\neq0$，$\mathrm{(f)}$～$\mathrm{(h)}$ では $z\neq0$ かつ $w\neq0$ とする．$0$ の絶対値 $|0|$ はもちろん $0$ であるが，
$0$ の偏角は通常定義されない．
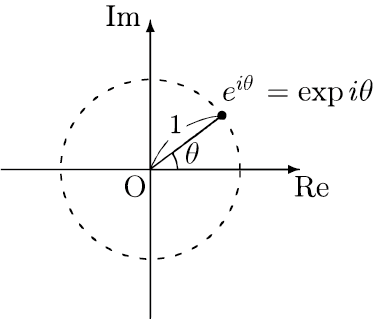
Eulerの公式
$\theta$ を任意の実数とするとき，$\cos\theta+i\sin\theta$ は絶対値 $1$，偏角 $\theta$ の複素数を表すが，この複素数を
$e^{i\theta}\stackrel{\mathrm{def}}{=}\cos{\theta}+i\sin\theta$
と表す．$e^{i\theta}$ のことを $\exp{i\theta}$ とも書く
(もちろん $e^{\theta i}$，$\exp{\theta i}$ と書いてもよい)．
複素平面上では，$e^{i\theta}$ は単位円周上の点である．
この等式は「Eulerの公式」と呼ばれる．定義なのに「公式」とは奇妙に感じられるであろう．実際，複素関数としての指数関数 $e^z$ を別に定義したうえでこの「公式」が成り立つことを証明する，という流儀もあり，そのほうが都合がいい面もあるが，ここではこの等式を定義として採用することにする．後述するが，我々はここでの「定義」をもとに複素関数としての指数関数 $e^z$ を考えていくことになる．
この表記を用いると，絶対値 $r$，偏角 $\theta$ の複素数は
$re^{i\theta}$ あるいは $r\exp{i\theta}$
と表される．この表し方を複素数の
極形式という．
上の例で見た複素数 $1+i$ と $-\sqrt{3}-i$ を偏角の範囲を $[0,2\pi)$ として極形式で表すと，それぞれ
$1+i=\sqrt{2}e^{\frac{\pi}{4}i}=\sqrt{2}\exp\dfrac{\pi}{4}i$
$-\sqrt{3}-i=2e^{\frac{7}{6}\pi i}=2\exp\dfrac{7}{6}\pi i$
となる．偏角の範囲を $(-\pi,\pi]$ に指定することも多いが，その場合は $-\sqrt{3}-i$ は
$-\sqrt{3}-i=2e^{-\frac{5}{6}\pi i}=2\exp\Big(-\dfrac{5}{6}\pi i\Big)$
となる．このように，偏角のとり方が一意ではないので，極形式の表し方も一意ではない．
すなわち、実部を横軸(実軸)上に、虚部を縦軸(虚軸)上にとり，複素数を平面上の点と見なすのである．
この表記を用いると，絶対値 $r$，偏角 $\theta$ の複素数は