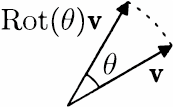第2講 実2次正方行列の逆行列,行列とベクトル
行列式
実 $2\times2$ 行列 $A=\left(\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\right)$ に対して,式 $a_{11}a_{22}-a_{12}a_{21}$ を $A$ の
行列式と呼び $|A|$,$\det{A}$,$\left|\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\right|$などと表す:
$|A|=\det{A}=\left|\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\right|=a_{11}a_{22}-a_{12}a_{21}$
$A=\left(\begin{array}{cc}3&1\\2&5\end{array}\right)$,
$B=\left(\begin{array}{cc}-2&6\\1&-3\end{array}\right)$ とすると
$|A|=\det{A}=\left|\begin{array}{cc}3&1\\2&5\end{array}\right|=3\cdot5-1\cdot2=13$
$|B|=\det{B}=\left|\begin{array}{cc}-2&6\\1&-3\end{array}\right|=(-2)\cdot(-3)-6\cdot1=0$
行列式を表す $|\cdots|$ の表記を
実数や複素数の絶対値記号と混同しないよう注意しよう.どちらもよく用いられるのであるが,本講座ではできるだけ "$|A|$" のような表記は避けて "$\det{A}$" と書くことにする.
行列式について,次は一般に成り立つか?
$\mathrm{(a)}$ $A\neq O$ ならば $|A|>0$
$\mathrm{(b)}$ $|A+B|\le |A|+|B|$
ともに成り立たない.これらは絶対値に関する性質なので行列式とは無関係である.反例は
| $\mathrm{(a)}$ |
$\left|\begin{array}{cc}0&1\\1&0\end{array}\right|=-1$
|
| $\mathrm{(b)}$ |
$A=\left(\begin{array}{cc}1&0\\0&0\end{array}\right)$,
$B=\left(\begin{array}{cc}0&0\\0&1\end{array}\right)$
とすると
$|A|+|B|=0+0=0$ であるが $|A+B|=\left|\begin{array}{cc}1&0\\0&1\end{array}\right|=1$ |
など.
逆行列
$A$ を実 $2$ 次正方行列,$E$ を $2$ 次の単位行列とするとき
$AA^{-1}=A^{-1}A=E$
を満たす行列 $A^{-1}$ を $A$ の
逆行列という.
行列 $A=\left(\!\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\!\right)$
の逆行列は,$\det{A}\neq0$ ならば
$\left(\!\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\!\right)^{-1}
=\dfrac{1}{\det{A}}\left(\!\begin{array}{cc}a_{22}&-a_{12}\\-a_{21}&a_{11}\end{array}\!\right)$
で与えられる.$\det{A}=0$ のときは逆行列は存在しない
詳しく!.
次が成り立つことを確かめよう:
$\left(\!\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\!\right)
\left(\!\begin{array}{cc}a_{22}&-a_{12}\\-a_{21}&a_{11}\end{array}\!\right)
$$=\left(\!\begin{array}{cc}a_{11}a_{22}-a_{12}a_{21}&0\\0&a_{11}a_{22}-a_{12}a_{21}\end{array}\!\right)$
$\left(\!\begin{array}{cc}a_{22}&-a_{12}\\-a_{21}&a_{11}\end{array}\!\right)
\left(\!\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\!\right)
$$=\left(\!\begin{array}{cc}a_{11}a_{22}-a_{12}a_{21}&0\\0&a_{11}a_{22}-a_{12}a_{21}\end{array}\!\right)$
これらより,$a_{11}a_{22}-a_{12}a_{21}\neq0$ ならば,それぞれ両辺を除することにより逆行列が存在して
$\left(\!\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\!\right)^{-1}
=\dfrac{1}{a_{11}a_{22}-a_{12}a_{21}}\left(\!\begin{array}{cc}a_{22}&-a_{12}\\-a_{21}&a_{11}\end{array}\!\right)$
となり,$a_{11}a_{22}-a_{12}a_{21}=0$ ならば逆行列は存在しないことがわかる.
行列$A=\left(\!\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\!\right)$ に対して
$\tilde{A}=\left(\!\begin{array}{cc}a_{22}&-a_{12}\\-a_{21}&a_{11}\end{array}\!\right)$
とおくと,上で見た計算は
$A\tilde{A}=\tilde{A}A=(\det{A})E$
と表される
(後述するが,この $\tilde{A}$ は $A$ の
余因子行列と呼ばれる).
従って,もし $\det{A}\neq0$ ならば$A^{-1}$が存在して
$A^{-1}=\dfrac{1}{\det{A}}\tilde{A}$
となる.もし $\det{A}=0$ ならば
$A\tilde{A}=\tilde{A}A=O$
ということになるが,にもかかわらず $A^{-1}$ が存在したとすると,
$A\tilde{A}=O$ の両辺に $A^{-1}$ を左から掛けることにより
$\tilde{A}=O$ となってしまう.
これは,$a_{11}=a_{12}=a_{21}=a_{22}=0$,すなわち $A=O$ であることを意味し,
零行列が逆行列をもつはずはない(零行列にいかなる行列を掛けても零行列である)ので矛盾である.
余因子行列に触れたついでに,
逆行列は存在すれば唯一つに定まること,すなわち,$2\times 2$ 行列 $A$ に対して
$AB=E$ となる行列 $B$ が存在すれば $B=\dfrac{1}{\det{A}}\tilde{A}$ である
ことも確認しておこう.
実際,$AB=E$ の両辺に左から $\tilde{A}$ を掛けることにより $(\det{A})B=\tilde{A}$ が得られるが,もし $\det{A}=0$ ならば $\tilde{A}=O$ となり上で見たとおりこれは $A=O$ を意味し,$AB=E$ とは両立し得ない.
よって $B=\dfrac{1}{\det{A}}\tilde{A}$ でありこれは $BA=E$ も満たし,$A$ の逆行列である.
もちろん,
$BA=E$ となる行列 $B$ が存在すれば $B=\dfrac{1}{\det{A}}\tilde{A}$ である
ということも同様に成り立つ.
$A=\left(\begin{array}{cc}3&1\\2&5\end{array}\right)$,
$B=\left(\begin{array}{cc}-2&6\\1&-3\end{array}\right)$ とすると
$\det{A}=13$ なので $A^{-1}$ は存在して
$A^{-1}=\dfrac{1}{13}\left(\begin{array}{cc}5&-1\\-2&3\end{array}\right)$
であり,$\det{B}=0$ なので $B^{-1}$ は存在しない.
逆行列を持つ行列を
正則行列という.すなわち
$A$ が正則 $\Leftrightarrow A^{-1}$ が存在する $\Leftrightarrow \det{A}\neq0$
二つの行列 $A$,$B$ がともに正則であれば,積 $AB$ も正則であり,従って逆行列を持つが,計算の際は積の順序に注意:
$(AB)^{-1}=B^{-1}A^{-1}$
実際
$AB(B^{-1}A^{-1})=(B^{-1}A^{-1})AB=E$ が成り立つことは容易に確認できよう.
細かいことを言うようだが,
$AB(B^{-1}A^{-1})=A(BB^{-1})A^{-1}=AA^{-1}=E$
$(B^{-1}A^{-1})AB=B^{-1}(A^{-1}A)B=B^{-1}B=E$
のような計算が許されるのは,行列の演算において
積に関する結合法則が成り立つからだということは意識しておいたほうがよいだろう.
すなわち,行列の掛け算は,(順序を入れ替えてはいけないが)どこから掛けてもよいのである.
$A$ が正則であり, $B$ が正則でないとき,積 $AB$ または $BA$ が正則となることはあるか?
ない.
もし $AB$ が正則ならば,逆行列 $(AB)^{-1}$ が存在して
$AB(AB)^{-1}=E$
が成り立つが,この両辺に
左から $A^{-1}$ を掛けて
$B(AB)^{-1}=A^{-1}$
さらに両辺に
右から $A$ を掛けて
$B(AB)^{-1}A=E$
となり,$(AB)^{-1}A$ が $B$ の逆行列(従って $B$ は正則)ということになってしまう.$BA$ についても同様.
(注)
実は,行列式には
$\det(AB)=\det{A}\det{B}$
が一般に成り立つという性質があり(後述),このことからも
$\det{B}=0$ ならば $\det(AB)=\det(BA)=0$
とわかる.
行列とベクトル
行列の役割は,ベクトルに作用して新しいベクトルに変換することである.
すなわち
$\left(\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\right)\left(\begin{array}{c}x_1\\x_2\end{array}\right)
=
\left(\begin{array}{c}a_{11}x_1+a_{12}x_2\\a_{21}x_1+a_{22}x_2\end{array}\right)$
という演算規則により,行列 $A$ はベクトル $\mathbf{x}$ をベクトル $A\mathbf{x}$ に変換する.このような,行列によるベクトルの変換は
線型変換,
一次変換などと呼ばれる.
$A=\left(\begin{array}{cc}1&3\\2&6\end{array}\right)$,
$\mathbf{x}=\left(\begin{array}{c}1\\1\end{array}\right)$,
$\mathbf{y}=\left(\begin{array}{c}3\\-1\end{array}\right)$ とすると
$A\mathbf{x}
=\left(\begin{array}{cc}1&3\\2&6\end{array}\right)
\left(\begin{array}{c}1\\1\end{array}\right)
=\left(\begin{array}{c}4\\8\end{array}\right)$
$A\mathbf{y}
=\left(\begin{array}{cc}1&3\\2&6\end{array}\right)
\left(\begin{array}{c}3\\-1\end{array}\right)
=\left(\begin{array}{c}0\\0\end{array}\right)$
すなわち,この行列 $A$ は
ベクトル $\left(\begin{array}{c}1\\1\end{array}\right)$ を
ベクトル $\left(\begin{array}{c}4\\8\end{array}\right)$ に,
ベクトル $\left(\begin{array}{c}3\\-1\end{array}\right)$ を
零ベクトル $\left(\begin{array}{c}0\\0\end{array}\right)$ に,
それぞれ変換する.
ここで言っている「ベクトル」とは,詳しくは
$2$ 次元実数ベクトル,すなわち二つの実数を成分とするベクトルのことである.
複素行列を扱うときは,ベクトルも複素数を成分に持つものを考えることになる.
ベクトルの回転
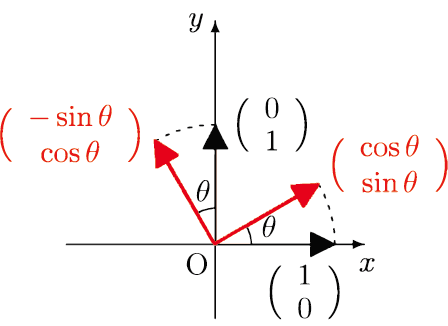
次の形の行列はベクトルを角 $\theta$ だけ回転させる変換を表す.
$\left(\begin{array}{cc}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right)$
この行列を $\mathrm{Rot}(\theta)$ と表すことにしよう.すなわち,任意に与えられたベクトル $\mathbf{v}$ に対して,$\mathrm{Rot}(\theta)\mathbf{v}$ は $\mathbf{v}$ と $\theta$ の角をなし.大きさ(長さ)は $\mathbf{v}$ と等しいベクトルである
詳しく!.
$\mathrm{Rot}(\theta)$ がに上の形に表されることを確かめるには,
角 $\theta$ の回転により
ベクトル $\left(\begin{array}{c}1\\0\end{array}\right)$ は
ベクトル $\left(\begin{array}{c}\cos\theta\\\sin\theta\end{array}\right)$ に,
ベクトル $\left(\begin{array}{c}0\\1\end{array}\right)$ は
ベクトル $\left(\begin{array}{c}-\sin\theta\\\cos\theta\end{array}\right)$ に移ることに注意すればよい.
すなわち
$\mathrm{Rot}(\theta)\left(\begin{array}{c}1\\0\end{array}\right)$
$=\left(\begin{array}{c}\cos\theta\\\sin\theta\end{array}\right)$
$\mathrm{Rot}(\theta)\left(\begin{array}{c}0\\1\end{array}\right)$
$=\left(\begin{array}{c}-\sin\theta\\\cos\theta\end{array}\right)$
の二式が成り立たなければならないが,これらは
$\mathrm{Rot}(\theta)\left(\begin{array}{cc}1&0\\0&1\end{array}\right)$
$=\left(\begin{array}{cc}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right)$
と一つの式にまとめられ,従って確かに
$\mathrm{Rot}(\theta)
=\left(\begin{array}{cc}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right)$
となる.
後に一般の場合について詳しく述べるが,
$2\times 2$ 行列は平行でない2本のベクトルの行き先で一意的に決まる
という事実は重要である.
その様子を簡単に見ておこう.
平行でない2本のベクトル
$\left(\begin{array}{c}a_1\\a_2\end{array}\right)$,
$\left(\begin{array}{c}b_1\\b_2\end{array}\right)$
の
$2\times 2$ 行列 $A$ による行き先が
$A\left(\begin{array}{c}a_1\\a_2\end{array}\right)=\left(\begin{array}{c}a'_1\\a'_2\end{array}\right)$,
$A\left(\begin{array}{c}b_1\\b_2\end{array}\right)=\left(\begin{array}{c}b'_1\\b'_2\end{array}\right)$
であったとする.この二式は
$A\left(\begin{array}{cc}a_1&b_1\\a_2&b_2\end{array}\right)=\left(\begin{array}{c}a'_1&b'_1\\a'_2&b'_2\end{array}\right)$
とまとめられるから
両辺に $\left(\begin{array}{cc}a_1&b_1\\a_2&b_2\end{array}\right)^{-1}$ を右から掛けることにより
$A=\left(\begin{array}{c}a'_1&b'_1\\a'_2&b'_2\end{array}\right)\left(\begin{array}{cc}a_1&b_1\\a_2&b_2\end{array}\right)^{-1}$
と,$A$ が定まることになる.
ここで,
$\left(\begin{array}{c}a_1\\a_2\end{array}\right)$ と
$\left(\begin{array}{c}b_1\\b_2\end{array}\right)$ が平行でないという条件が
すなわち $a_1b_2-a_2b_1\neq0$ ということであり,従って $\left(\begin{array}{cc}a_1&b_1\\a_2&b_2\end{array}\right)$ の逆行列がちゃんと存在していることに注意しよう.
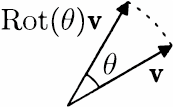
$xy$ 平面において,$(a,b)$ を座標として持つ点はしばしばその位置ベクトル $\left(\begin{array}{c}a\\b\end{array}\right)$ と同一視される.
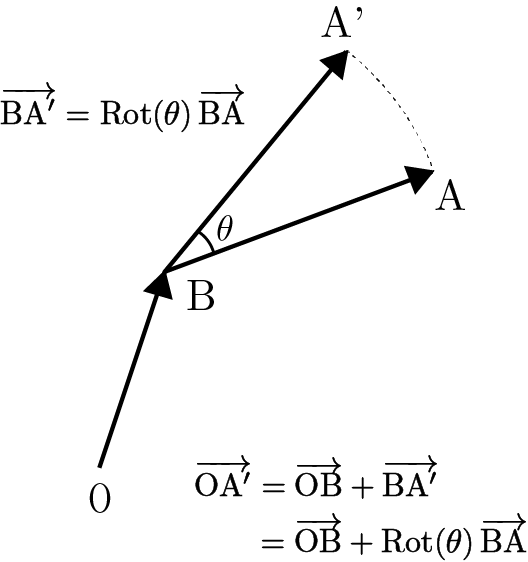
その観点から「座標平面における点の回転移動」を考えよう:
$\mathrm{O}$ を原点とする $xy$ 平面上において点 $\mathrm{A}$ を点 $\mathrm{B}$ を中心に角 $\theta$ だけ回転にした点を$\mathrm{A'}$とするとき,ベクトルの関係としては
$\overrightarrow{\mathrm{BA'}}=\mathrm{Rot}(\theta)\,\overrightarrow{\mathrm{BA}}$
が成り立つ.従って点 $\mathrm{A'}$ の位置ベクトルは
$\overrightarrow{\mathrm{OA'}}
=\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{BA'}}
=\overrightarrow{\mathrm{OB}}+\mathrm{Rot}(\theta)\,\overrightarrow{\mathrm{BA}}$
と計算されることになる.
-
点 $\mathrm{A}(1,1)$ を原点 $\mathrm{O}(0,0)$ を中心に角 $\dfrac{\pi}{3}$ 回転させた点を $\mathrm{A'}$ とすると
| $\overrightarrow{\mathrm{OA'}}$ |
$=\mathrm{Rot}\Big(\dfrac{\pi}{3}\Big)\overrightarrow{\mathrm{OA}}$
|
|
$=\left(\begin{array}{cc}1/2&-\sqrt{3}/2\\\sqrt{3}/2&1/2\end{array}\right)
\left(\begin{array}{c}1\\1\end{array}\right)$
$=\dfrac{1}{2}\left(\begin{array}{c}1-\sqrt{3}\\\sqrt{3}+1\end{array}\right)$
|
より,点 $\mathrm{A'}$ の座標は $\Big(\dfrac{1-\sqrt{3}}{2},\dfrac{\sqrt{3}+1}{2}\Big)$.
-
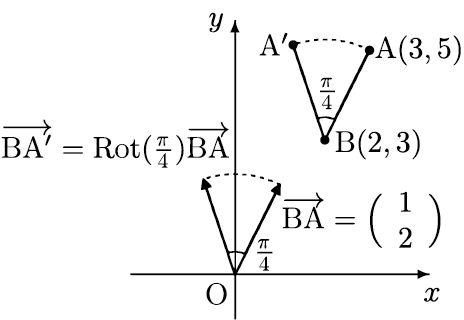
点 $\mathrm{A}(3,5)$ を点 $\mathrm{B}(2,3)$ を中心に角 $\dfrac{\pi}{4}$ 回転させた点を $\mathrm{A'}$ とすると,
$\overrightarrow{\mathrm{BA}}=\left(\begin{array}{c}1\\2\end{array}\right)$ ゆえ
| $\overrightarrow{\mathrm{BA'}}$ |
$=\mathrm{Rot}\Big(\dfrac{\pi}{4}\Big)\overrightarrow{\mathrm{BA}}$
|
|
$=\left(\begin{array}{cc}1/\sqrt{2}&-1/\sqrt{2}\\1/\sqrt{2}&1/\sqrt{2}\end{array}\right)
\left(\begin{array}{c}1\\2\end{array}\right)$
$=\dfrac{1}{\sqrt{2}}\left(\begin{array}{c}-1\\3\end{array}\right)$
|
よって
| $\overrightarrow{\mathrm{OA'}}$ |
$=\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{BA'}}$
|
|
$=\left(\begin{array}{c}2\\3\end{array}\right)+\dfrac{1}{\sqrt{2}}\left(\begin{array}{c}-1\\3\end{array}\right)$
$=\left(\begin{array}{c}2-1/\sqrt{2}\\3+3/\sqrt{2}\end{array}\right)$
|
より,点 $\mathrm{A'}$ の座標は $\Big(2-\dfrac{1}{\sqrt{2}},3+\dfrac{3}{\sqrt{2}}\Big)$.
連立一次方程式
二元連立一次方程式
$\left\{\begin{array}{l}ax+by=p\\cx+dy=q\end{array}\right.$
は,行列とベクトルを用いて
$\left(\begin{array}{cc}a&b\\c&d\end{array}\right)
\left(\begin{array}{c}x\\y\end{array}\right)
=\left(\begin{array}{c}p\\q\end{array}\right)$
と表すことができる.従って,もし係数行列 $\left(\begin{array}{cc}a&b\\c&d\end{array}\right)$ が逆行列を持つならば,それを両辺に左から掛けることによって
$\left(\begin{array}{c}x\\y\end{array}\right)
=\left(\begin{array}{cc}a&b\\c&d\end{array}\right)^{-1}\left(\begin{array}{c}p\\q\end{array}\right)$
として解を求めることができる.
逆行列を持たない場合も含め,一般の連立一次方程式の取り扱いについては後述する.
連立一次方程式
$\left\{\begin{array}{l}2x+y=3\\3x+5y=-1\end{array}\right.$
は
$\left(\begin{array}{cc}2&1\\3&5\end{array}\right)
\left(\begin{array}{c}x\\y\end{array}\right)
=\left(\begin{array}{c}3\\-1\end{array}\right)$
と表せるので,
|
$\left(\begin{array}{c}x\\y\end{array}\right)$ |
$=\left(\begin{array}{cc}2&1\\3&5\end{array}\right)^{-1}
\left(\begin{array}{c}3\\-1\end{array}\right)$
$=\dfrac{1}{7}\left(\begin{array}{cc}5&-1\\-3&2\end{array}\right)
\left(\begin{array}{c}3\\-1\end{array}\right)
=\dfrac{1}{7}\left(\begin{array}{c}16\\-11\end{array}\right)$
|
より,解は $(x,y)=\Big(\dfrac{16}{7},-\dfrac{11}{7}\Big)$.
このように,連立一次方程式とは,与えられた行列 $A$ とベクトル $\mathbf{b}$ に対して
$A\mathbf{x}=\mathbf{b}$ を満たすようなベクトル $\mathbf{x}$ を求める問題であって,もし $A$ が逆行列を持つならば,それを方程式の両辺に左から掛けることによって
$A^{-1}A\mathbf{x}=A^{-1}\mathbf{b}$
から $\mathbf{x}=A^{-1}\mathbf{b}$ と解を求めることができる.
ただし,ここでもうるさいことを言うと,行列 $A$,$B$ とベクトル $\mathbf{x}$ との演算に関しても
$A(B\mathbf{x})=(AB)\mathbf{x}$
という規則が成立することは証明を要するのであるが,それは行列の演算の一般論に含まれるのでここでは行わない.