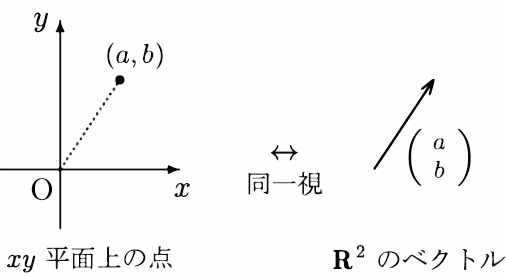
ベクトル空間$\mathbf{R}^2$
$2$ 次元実数ベクトルは,二つの実数 $x,y$ により $\left(\begin{array}{c}x\\y\end{array}\right)$ と表されるのであった.これらをすべて集めた集合を
$\mathbf{R}^2=\left\{\left.\, \left(\begin{array}{c}x\\y\end{array}\right)\ \right|\ x,y\in\mathbf{R}\ \right\}$
と書き,$2$ 次元
実数ベクトル空間という.
当たり前ではあるが,次が成り立つことに注意しておこう.
$\left(\begin{array}{c}a_1\\a_2\end{array}\right),\ \left(\begin{array}{c}b_1\\b_2\end{array}\right)\in\mathbf{R}^2
\ \Rightarrow\
\left(\begin{array}{c}a_1\\a_2\end{array}\right)+\left(\begin{array}{c}b_1\\b_2\end{array}\right)\in\mathbf{R}^2$
$\left(\begin{array}{c}a_1\\a_2\end{array}\right)\in\mathbf{R}^2,\ k\in\mathbf{R}
\ \Rightarrow\
k\left(\begin{array}{c}a_1\\a_2\end{array}\right)\in\mathbf{R}^2$
一般に,「ベクトル空間」とは,この $\mathbf{R}^2$ のように和とスカラー倍という演算が定義されている集合のことを指す(詳しくは後述).
二つの複素数を並べて表されるベクトルは $2$ 次元複素数ベクトルと呼んでもよいが,単に
$2$ 次元数ベクトルと呼ばれることが多い(単に「数」と言うときは複素数を指す習慣である).
それらをすべて集めた集合
$\mathbf{C}^2=\left\{\left.\, \left(\begin{array}{c}z\\w\end{array}\right)\ \right|\ z,w\in\mathbf{C}\ \right\}$
は
$2$ 次元数ベクトル空間と呼ばれる.
一般に,「ベクトル」とは(雑に言うと)和とスカラー倍が定義されているもののことをいう.
例えば,数列や関数などもベクトルとして扱うことができる.
ここで見ているような「数」を並べて表されるベクトルは,特に「数ベクトル」と呼ばれるのである.
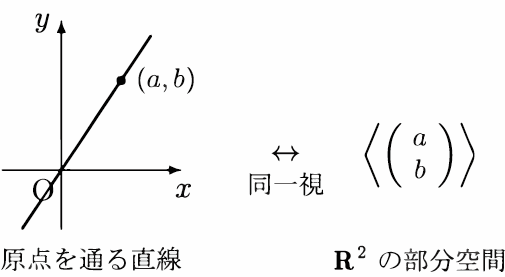
$\mathbf{R}^2$の部分空間
$W$ が $\mathbf{R}^2$ の部分集合であって,$W$ 自体もベクトル空間となっているとき,すなわち
$\mathrm{(i)}$ $\mathbf{a},\ \mathbf{b}\in W\ \Rightarrow \mathbf{a}+\mathbf{b}\in W$
$\mathrm{(ii)}$ $\mathbf{a}\in W,\ k\in\mathbf{R}\ \Rightarrow k\mathbf{a}\in W$
が成り立つとき,
$W$ を $\mathbf{R}^2$ の
部分空間(部分ベクトル空間)という.
この二つの条件 $\mathrm{(i)}$,$\mathrm{(ii)}$ は
$\mathrm{(iii)}$ $\mathbf{a},\ \mathbf{b}\in W,\ k,l\in\mathbf{R}\ \Rightarrow k\mathbf{a}+l\mathbf{b}\in W$
と一つにまとめることもできる
詳しく!
.
$\mathrm{(i)},\ \mathrm{(ii)}\ \Rightarrow \mathrm{(iii)}$
$\mathrm{(i)},\ \mathrm{(ii)}$が成り立つと仮定し,
$\mathbf{a},\ \mathbf{b}\in W,\ k,l\in\mathbf{R}$
とすると,まず $\mathrm{(ii)}$ より $k\mathbf{a},\ l\mathbf{b}\in W$ さらに $\mathrm{(i)}$ より $k\mathbf{a}+l\mathbf{b}\in W$ となる.よって $\mathrm{(iii)}$ が成り立つ.
$\mathrm{(iii)}\ \Rightarrow \mathrm{(i)},\ \mathrm{(ii)}$
$\mathrm{(iii)}$ が成り立つと仮定し,
$\mathbf{a},\ \mathbf{b}\in W$ とすると,
$\mathbf{a}+\mathbf{b}=1\mathbf{a}+1\mathbf{b}\in W$ となり,$\mathrm{(i)}$ が成り立つ.
また,$\mathbf{a}\in W,\ k\in\mathbf{R}$ とすると
,$k\mathbf{a}=k\mathbf{a}+0\mathbf{a}\in W$ となり,$\mathrm{(ii)}$ が成り立つ.
- ベクトル $\left(\begin{array}{c}1\\2\end{array}\right)$
と平行なすべてのベクトルからなる集合
$W_1=\left\{\left.\, t\left(\begin{array}{c}1\\2\end{array}\right)\ \right|\ t\in\mathbf{R}\ \right\}$
は $\mathbf{R}^2$ の部分空間である.
実際,$\mathbf{a}$,$\mathbf{b}\in W_1$ とすると
$\mathbf{a}=s\left(\begin{array}{c}1\\2\end{array}\right)$,
$\mathbf{b}=t\left(\begin{array}{c}1\\2\end{array}\right)$ $(s,t\in\mathbf{R})$ と表せるから
$\mathbf{a}+\mathbf{b}=(s+t)\left(\begin{array}{c}1\\2\end{array}\right)\in W_1$
であり,
また,任意のスカラー $k\in\mathbf{R}$ に対して
$k\mathbf{a}=ks\left(\begin{array}{c}1\\2\end{array}\right)\in W_1$
となっている.このような状況を,$W_1$ は「和,スカラー倍に関して閉じている」と言い表す.
-
第2成分が第1成分より $1$ だけ大きいようなベクトルからなる集合
$W_2=\left\{\left.\, \left(\begin{array}{c}x\\y\end{array}\right)\ \right|\ y=x+1\ \right\}$
は部分空間ではない.例えば,
$\mathbf{a}'=\left(\begin{array}{c}0\\1\end{array}\right)$,$\mathbf{b}'=\left(\begin{array}{c}1\\2\end{array}\right)$
とすると $\mathbf{a}',\mathbf{b}'\in W_2$ であるが
$\mathbf{a}'+\mathbf{b}'=\left(\begin{array}{c}1\\3\end{array}\right)\notin W_2$
だから,$W_2$ は和に関して閉じていない.
あるいは
$2\mathbf{a}=\left(\begin{array}{c}0\\2\end{array}\right)\notin W_2$
だから,$W_2$ はスカラー倍に関しても閉じていない.
$\mathbf{R}^2$ の部分空間で自明
何?
$\mathbf{R}^2$ 自身,および零ベクトル $\mathbf{0}=\left(\begin{array}{c}0\\0\end{array}\right)$ のみを含む集合 $\{\,\mathbf{0}\,\}$ の二つは明らかに条件を満たすので「自明な部分空間」と言われる.
でないものは,
零ベクトルでないある一つのベクトル $\left(\begin{array}{c}a\\b\end{array}\right)$ と平行なすべてのベクトルからなる集合であり,
$\left\langle\left(\begin{array}{c}a\\b\end{array}\right)\right\rangle$ と表される:
$\left\langle\left(\begin{array}{c}a\\b\end{array}\right)\right\rangle
\stackrel{\mathrm{def}}{=}\left\{\left.t\left(\begin{array}{c}a\\b\end{array}\right)\right|\ t\in\mathbf{R}\ \right\}$
以下,「ベクトル $\mathbf{a}$ と平行なベクトル」とは,$t\mathbf{a}$ ($t\in\mathbf{R}$) と表されるベクトルのことを指す.従って零ベクトル $\mathbf{0}=\left(\begin{array}{c}0\\0\end{array}\right)$ も含む.
「次元」について詳しくは後述するが,この空間は一つのベクトルを用いて表されるという意味で
$1$ 次元部分空間である
詳しく!
.
零ベクトル $\mathbf{0}$ のみからなる部分空間 $\{\,\mathbf{0}\,\}$ の次元は $0$ と規約する.
また,全空間 $\mathbf{R}^2$ は $2$ 次元空間である.
その意味は,$\mathbf{R}^2$ のすべてのベクトルを表すのに $2$ 本のベクトルが必要($3$ 本は必要ない)ということである.
例えば,
$\mathbf{a}=\left(\begin{array}{c}1\\1\end{array}\right)$,
$\mathbf{b}=\left(\begin{array}{c}2\\3\end{array}\right)$ とすると,
$\mathbf{R}^2$ のすべてのベクトルは $\mathbf{a}$,$\mathbf{b}$ の
線型結合(次項)で表される.すなわち,
任意の $\left(\begin{array}{c}p\\q\end{array}\right)\in\mathbf{R}^2$
に対して
$\left(\begin{array}{c}p\\q\end{array}\right)=t_1\left(\begin{array}{c}1\\1\end{array}\right)+t_2\left(\begin{array}{c}2\\3\end{array}\right)
$
を満たすスカラー(実数) $t_1,t_2$ が必ず存在する
さらに詳しく!
.
実際,この式を行列を用いて表すと
$\left(\begin{array}{cc}1&2\\1&3\end{array}\right)\left(\begin{array}{c}t_1\\t_2\end{array}\right)=
\left(\begin{array}{c}p\\q\end{array}\right)$
となり,係数行列 $\left(\begin{array}{cc}1&2\\1&3\end{array}\right)$ は逆行列を持つから,それを両辺に左から掛けることにより
$\left(\begin{array}{c}t_1\\t_2\end{array}\right)
=\left(\begin{array}{cc}1&2\\1&3\end{array}\right)^{-1}\left(\begin{array}{c}p\\q\end{array}\right)$
と,$t_1,t_2$ が定まる.
上の議論において,$\left(\begin{array}{cc}1&2\\1&3\end{array}\right)$ が逆行列を持つのは,$\left(\begin{array}{c}1\\1\end{array}\right)$ と $\left(\begin{array}{c}2\\3\end{array}\right)$ が
互いに平行でないからだということに注意しよう.
一般に,行列 $A=\left(\begin{array}{cc}a&b\\c&d\end{array}\right)$ について
$A$ が逆行列を持つ
$\hspace{15pt}\Leftrightarrow\ ad-bc\neq0$
$\hspace{15pt}\Leftrightarrow\left(\begin{array}{c}a\\c\end{array}\right)$ と
$\left(\begin{array}{c}b\\d\end{array}\right)$ は互いに平行でない
が成り立つのであった.
このことを踏まえ,
$\mathbf{R}^2$ の部分空間 $W$ は
$\mathbf{a},\mathbf{b}\in W,\ t_1,t_2\in\mathbf{R}\ \Rightarrow t_1\mathbf{a}+t_2\mathbf{b}\in W$
を満たさなければならないことを考えると,
$W$ が平行でない $2$ 本のベクトルを含むならば,$W$ は $\mathbf{R}^2$ のすべてのベクトルを含むことになり,結局
$W=\mathbf{R}^2$
となる.従って,$W$ が $\mathbf{R}^2$ でも $\{\,\mathbf{0}\,\}$ でもない非自明な部分空間であるためには,ある $1$ 本のベクトル $\mathbf{a}\ (\neq\mathbf{0})$ と,$\mathbf{a}$ と平行なベクトルしか含んではならない,すなわち
$W=\langle\mathbf{a}\rangle\stackrel{\mathrm{def}}{=}\{\,t\mathbf{a}\ |\ t\in\mathbf{R}\,\}$
と表されることがわかる.
さらに,この空間を
$\left\langle\left(\begin{array}{c}a\\b\end{array}\right)\right\rangle=
\left\{\left.\, \left(\begin{array}{c}x\\y\end{array}\right)\ \right|\ bx-ay=0\ \right\}$
という形で表すこともできる
詳しく!
.
実際,
$\left\langle\left(\begin{array}{c}a\\b\end{array}\right)\right\rangle
=\left\{\left.t\left(\begin{array}{c}a\\b\end{array}\right)\right|\ t\in\mathbf{R}\ \right\}\\[1mm]
\hspace{37pt}=\left\{\left.\left(\begin{array}{c}at\\bt\end{array}\right)\right|\ t\in\mathbf{R}\ \right\}$
から $x=at$,$y=bt$ とおき $t$ を消去すると $bx-ay=0$ が得られるから
$\left\langle\left(\begin{array}{c}a\\b\end{array}\right)\right\rangle
=\left\{\left.\, \left(\begin{array}{c}x\\y\end{array}\right)\ \right|\ bx-ay=0\ \right\}$
と表される.
ここに現れた $bx-ay=0$ という式は $xy$ 平面において原点および点 $(a,b)$ を通る直線を表すので,
$xy$ 平面上の点とその位置ベクトルを同一視する観点から
| $xy$ 平面全体 | $\quad\leftrightarrow\quad$ | 全空間 $\mathbf{R}^2$ |
| 原点および点 $(a,b)$ を通る直線 | $\quad\leftrightarrow\quad$ | $1$ 次元部分空間 $\left\langle\left(\begin{array}{c}a\\b\end{array}\right)\right\rangle$ |
| 原点 | $\quad\leftrightarrow\quad$ | $0$ 次元部分空間 $\{\,\mathbf{0}\,\}$ |
と見なすことができる.
このような図形的な把握の仕方は,先々 $4$ 次元以上も含めた一般論になると通用しなくなるが,
だとしても,低次元における図形的イメージを持っておくことは,抽象概念を理解する手掛かりとして有効である.
次のうち,部分空間
$\left\langle\left(\begin{array}{c}4\\3\end{array}\right)\right\rangle$
と同じものはどれか?
$\mathrm{(a)}$ $\left\langle\left(\begin{array}{c}8\\6\end{array}\right)\right\rangle$
$\mathrm{(b)}$ $\left\langle\left(\begin{array}{c}-4\\-3\end{array}\right)\right\rangle$
$\mathrm{(c)}$ $\left\{\left.\, \left(\begin{array}{c}x\\y\end{array}\right)\ \right|\ 3x-4y=0\ \right\}$
$\mathrm{(d)}$ $\left\{\left.\, \left(\begin{array}{c}x\\y\end{array}\right)\ \right|\ y=\dfrac{3}{4}x\ \right\}$
すべて.
部分空間の生成
一般に,ベクトル $\mathbf{a}_1,\mathbf{a}_2,\ldots,\mathbf{a}_n$ が与えられたとき,スカラー(実数) $t_1,t_2,\ldots,t_n$ により
$t_1\mathbf{a}_1+t_2\mathbf{a}_2+\ldots+t_n\mathbf{a}_n$
の形で表されるベクトルを $\mathbf{a}_1,\mathbf{a}_2,\ldots,\mathbf{a}_n$ の
線型結合(一次結合)というが,それらをすべて集めた集合を
$\mathbf{a}_1,\mathbf{a}_2,\ldots,\mathbf{a}_n$ が
生成する(張る)部分空間といい,$\langle\mathbf{a}_1,\mathbf{a}_2,\ldots,\mathbf{a}_n\rangle$ と表す:
$\langle\mathbf{a}_1,\mathbf{a}_2,\ldots,\mathbf{a}_n\rangle$
$\stackrel{\mathrm{def}}{=}\{\,t_1\mathbf{a}_1+t_2\mathbf{a}_2+\ldots+t_n\mathbf{a}_n\ |\ t_1,t_2\ldots,t_n\in\mathbf{R}\,\}$
もし $\mathbf{a},\mathbf{b}\in\mathbf{R}^2$ であって,$\mathbf{b}$ が $\mathbf{a}$ と平行ならば
$\langle\mathbf{a},\mathbf{b}\rangle=\langle\mathbf{a}\rangle$
であることに注意しよう
詳しく!.
例えば,
$\mathbf{a}=\left(\begin{array}{c}1\\2\end{array}\right)$,
$\mathbf{b}=\left(\begin{array}{c}2\\4\end{array}\right)$ とすると
$\left\langle\mathbf{a},\mathbf{b}\right\rangle
=\left\{\left.t_1\left(\begin{array}{c}1\\2\end{array}\right)+t_2\left(\begin{array}{c}2\\4\end{array}\right)\right|\ t_1,t_2\in\mathbf{R}\ \right\}\\[1mm]
\hspace{23pt}=\left\{\left.(t_1+2t_2)\left(\begin{array}{c}1\\2\end{array}\right)\right|\ t_1,t_2\in\mathbf{R}\ \right\}$
$\left\langle\mathbf{a}\right\rangle
=\left\{\left.t\left(\begin{array}{c}1\\2\end{array}\right)\right|\ t\in\mathbf{R}\ \right\}$
であるが,これらはいずれも $\left(\begin{array}{c}1\\2\end{array}\right)$ と平行なすべてのベクトルからなる集合である.
同様に考えて,$\mathbf{R}^2$ の $n$ 個のベクトル $\mathbf{b_1},\mathbf{b_2},\ldots,\mathbf{b}_n$ がすべて $\mathbf{a}$ と平行ならば
$\langle\mathbf{a},\mathbf{b_1},\mathbf{b_2},\ldots,\mathbf{b}_n\rangle=
\langle\mathbf{a}\rangle$
となることがわかる.
次のうち,部分空間
$\left\langle\left(\begin{array}{c}3\\-1\end{array}\right)\right\rangle$
と同じものはどれか?
$\mathrm{(a)}$ $\left\langle\left(\begin{array}{c}6\\-2\end{array}\right)\right\rangle$
$\mathrm{(b)}$ $\left\langle\left(\begin{array}{c}-3\\1\end{array}\right),\ \left(\begin{array}{c}12\\-4\end{array}\right)\right\rangle$
$\mathrm{(c)}$ $\left\langle\left(\begin{array}{c}15\\-5\end{array}\right),\ \left(\begin{array}{c}0\\0\end{array}\right)\right\rangle$
$\mathrm{(d)}$ $\left\langle\left(\begin{array}{c}3\\-1\end{array}\right),\ \left(\begin{array}{c}1\\-1/3\end{array}\right),\,\ \left(\begin{array}{c}3\sqrt{2}\\-\sqrt{2}\end{array}\right)\right\rangle$
すべて.
また,$\mathbf{a},\mathbf{b}\in\mathbf{R}^2$ が互いに平行でないならば
$\langle\mathbf{a},\mathbf{b}\rangle=\mathbf{R}^2$
である
詳しく!.
例えば,
$\mathbf{a}=\left(\begin{array}{c}1\\1\end{array}\right)$,
$\mathbf{b}=\left(\begin{array}{c}2\\3\end{array}\right)$ とすると,
$\left\langle\mathbf{a},\mathbf{b}\right\rangle$ はこれら平行でない二本のベクトルを含むことになるので,前項で見たように全空間 $\mathrm{R}^2$ と一致する.
実際,
$\left\langle\mathbf{a},\mathbf{b}\right\rangle
=\left\{\left.t_1\left(\begin{array}{c}1\\1\end{array}\right)+t_2\left(\begin{array}{c}2\\3\end{array}\right)\right|\ t_1,t_2\in\mathbf{R}\ \right\}$
であるが,$\left(\begin{array}{c}1\\1\end{array}\right)$ と $\left(\begin{array}{c}2\\3\end{array}\right)$ が平行でないことから,
$\mathbf{R}^2$ のすべてのベクトル $\left(\begin{array}{c}p\\q\end{array}\right)$ は実数 $t_1$,$t_2$ を用いて
$\left(\begin{array}{c}p\\q\end{array}\right)=t_1\left(\begin{array}{c}1\\1\end{array}\right)+t_2\left(\begin{array}{c}2\\3\end{array}\right)
$
と表すことができるのであった.
従って,$\langle\mathbf{a},\mathbf{b}\rangle$ は $\mathbf{R}^2$ のベクトルをすべて含むような $\mathbf{R}^2$ の部分空間ということになり,それはすなわち
$\langle\mathbf{a},\mathbf{b}\rangle=\mathbf{R}^2$
を意味する.
同様に考えて,$\mathbf{R}^2$ の $n$ 個のベクトル $\mathbf{a_1},\mathbf{a_2},\ldots,\mathbf{a}_n$ の中に互いに平行でない組が一組でもあれば
$\langle\mathbf{a_1},\mathbf{a_2},\ldots,\mathbf{a}_n\rangle=
\mathbf{R}^2$
となる.
次のうち,$\mathrm{R}^2$ と同じものはどれか?
$\mathrm{(a)}$ $\left\langle\left(\begin{array}{c}1\\0\end{array}\right),\ \left(\begin{array}{c}0\\1\end{array}\right)\right\rangle$
$\mathrm{(b)}$ $\left\langle\left(\begin{array}{c}4\\-2\end{array}\right),\ \left(\begin{array}{c}-2\\1\end{array}\right)\right\rangle$
$\mathrm{(c)}$ $\left\langle\left(\begin{array}{c}1\\5\end{array}\right),\ \left(\begin{array}{c}0\\0\end{array}\right)\right\rangle$
$\mathrm{(d)}$ $\left\langle\left(\begin{array}{c}1\\1\end{array}\right),\ \left(\begin{array}{c}2\\2\end{array}\right),\,\ \left(\begin{array}{c}3\\4\end{array}\right)\right\rangle$
$\mathrm{(a)}$ と $\mathrm{(d)}$.
線型写像の像空間と階数
前講で述べたように,行列の役割はベクトルを新しいベクトルに変換することであった.特に,実 $2\times 2$ 行列 $A$ は,$\mathbf{R}^2$ のベクトル $\mathbf{x}$ を $\mathbf{R}^2$ のベクトル $A\mathbf{x}$ に変換する
線型写像(一次写像)を定める.この写像を $f_A$ と表すことにしよう:
$f_A(\mathbf{x})=A\mathbf{x}\quad(\mathbf{x}\in\mathbf{R}^2)$
ここで,写像 $f_A$ が「線型」であるとは
$f_A(\mathbf{x}_1+\mathbf{x}_2)=f_A(\mathbf{x}_1)+f_A(\mathbf{x}_2)\qquad(\mathbf{x}_1,\mathbf{x}_2\in\mathbf{R}^2)$
$f_A(k\mathbf{x})=kf_A(\mathbf{x})\qquad(\mathbf{x}\in\mathbf{R}^2,\ k\in\mathbf{R})$
が成り立つことをいう.一つにまとめて
$f_A(k_1\mathbf{x}_1+k_2\mathbf{x}_2)=k_1f_A(\mathbf{x}_1)+k_2f_A(\mathbf{x}_2)$$\hspace{100pt}(\mathbf{x}_1,\mathbf{x}_2\in\mathbf{R}^2,\ k_1,k_2\in\mathbf{R})$
が成り立つことだといってもよい.
簡単に言うと
和とスカラー倍という演算を,ベクトルを移す前に行っても移した後に行っても結果は同じ
であるような写像が線型写像である.
行列とベクトルの演算規則に基づいて
$A(k_1\mathbf{x}_1+k_2\mathbf{x}_2)=k_1A\mathbf{x}_1+k_2A\mathbf{x}_2$
が確かに成り立っていることを確認されたい.「スカラー倍して足す」という操作を,左辺では行列を掛ける前に,右辺は行列を掛けた後に行っているが,どちらでも結果は同じである.
$A=\left(\begin{array}{cc}1&2\\2&4\end{array}\right)$
$\mathbf{x}_1=\left(\begin{array}{c}1\\1\end{array}\right)$,
$\mathbf{x}_2=\left(\begin{array}{c}3\\-1\end{array}\right)$,
$\mathbf{0}=\left(\begin{array}{c}0\\0\end{array}\right)$
とするとき,$f_A(\mathbf{x}_1)$,$f_A(\mathbf{x}_2)$,$f_A(\mathbf{0})$ を求めよ.
$f(\mathbf{x}_1)
=\left(\begin{array}{cc}1&2\\2&4\end{array}\right)\left(\begin{array}{c}1\\1\end{array}\right)
=\left(\begin{array}{c}3\\6\end{array}\right)$
$f(\mathbf{x}_2)
=\left(\begin{array}{cc}1&2\\2&4\end{array}\right)\left(\begin{array}{c}3\\-1\end{array}\right)
=\left(\begin{array}{c}1\\2\end{array}\right)$
$f(\mathbf{0})
=\left(\begin{array}{cc}1&2\\2&4\end{array}\right)\left(\begin{array}{c}0\\0\end{array}\right)
=\left(\begin{array}{c}0\\0\end{array}\right)$
実 $2\times 2$ 行列 $A$ が定める線型写像 $f_A$ の像空間とは,$f_A$ によって移されたすべてのベクトルの集合であり,$\mathrm{Im}f_A$ と表す:
$\mathrm{Im}f_A
\stackrel{\mathrm{def}}{=}\{\,f_A(\mathbf{x})\ |\ \mathbf{x}\in\mathbf{R}^2\,\}
=\{\,A\mathbf{x}\ |\ \mathbf{x}\in\mathbf{R}^2\,\}$
$A=\left(\begin{array}{cc}a&b\\c&d\end{array}\right)$ とすると
$\mathrm{Im}f_A
=\left\langle\left(\begin{array}{c}a\\c\end{array}\right),\left(\begin{array}{c}b\\d\end{array}\right)\right\rangle$
である
詳しく!.
実際
$\mathrm{Im}f_A
=\{\,A\mathbf{x}\ |\ \mathbf{x}\in\mathbf{R}^2\,\}\\[1mm]
\hspace{22pt}=\left\{\left.\,\left(\begin{array}{cc}a&b\\c&d\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)\ \right|\ \left(\begin{array}{c}x\\y\end{array}\right)\in\mathbf{R}^2\,\right\}\\[1mm]
\hspace{22pt}=\left\{\left.\,\left(\begin{array}{c}ax+by\\cx+dy\end{array}\right)\ \right|\ x,y\in\mathbf{R}\,\right\}\\[1mm]
\hspace{22pt}=\left\{\left.\,x\left(\begin{array}{c}a\\c\end{array}\right)+y\left(\begin{array}{c}b\\d\end{array}\right)\ \right|\ x,y\in\mathbf{R}\,\right\}\\[1mm]
\hspace{22pt}=\left\langle\left(\begin{array}{c}a\\c\end{array}\right),\left(\begin{array}{c}b\\d\end{array}\right)\right\rangle$
となる.
この像空間 $f_A$ の次元のことを行列 $A$ の
階数といい,$\mathrm{rank}A$ で表す
(「線型写像 $f_A$ の階数」ともいい,$\mathrm{rank}f_A$ と表すこともある).
-
$A=\left(\begin{array}{cc}1&3\\2&6\end{array}\right)$ とすると($\det{A}=0$)
$\mathrm{Im}f_A
=\left\langle\left(\begin{array}{c}1\\2\end{array}\right),
\left(\begin{array}{c}3\\6\end{array}\right)\right\rangle
=\left\langle\left(\begin{array}{c}1\\2\end{array}\right)\right\rangle
$
となり,$\mathrm{Im}f_A$ は $1$ 次元部分空間である.
よって $\mathrm{rank}A=1$.
-
$B=\left(\begin{array}{cc}2&3\\2&1\end{array}\right)$ とすると($\det{B}\neq0$)
$\mathrm{Im}f_B
=\left\langle\left(\begin{array}{c}2\\2\end{array}\right),
\left(\begin{array}{c}3\\1\end{array}\right)\right\rangle
=\mathbf{R}^2
$
となり,$\mathrm{Im}f_B$ は $2$ 次元部分空間(全空間)である.
よって $\mathrm{rank}B=2$.
-
自明ではあるが,零行列
$O=\left(\begin{array}{cc}0&0\\0&0\end{array}\right)$ も見ておくと
$\mathrm{Im}f_O
=\left\langle\left(\begin{array}{c}0\\0\end{array}\right)\right\rangle
=\left\{\,\left(\begin{array}{c}0\\0\end{array}\right)\,\right\}
$
となり,これは $0$ 次元空間という規約であったから $\mathrm{rank}O=0$.