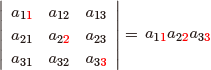第6講 対称群と行列式
置換
$n$ を$2$ 以上の自然数とするとき,集合 $\{\,1,2,\ldots,n\,\}$ から集合 $\{\,1,2,\ldots,n\,\}$ への全単射 $\sigma$ を $n$ 次の
置換といい,
$\sigma=\left(\begin{array}{cccc}1&2&\cdots&n\\ \sigma(1)&\sigma(2)&\cdots&\sigma(n)\end{array}\right)$
と表す.
行列と同じような表記を用いているが,置換は行列ではない.
混同しないように注意しよう.
$3$ 次の置換 $\sigma=\left(\begin{array}{ccc}1&2&3\\ 2&3&1\end{array}\right)$ は
$\sigma(1)=2$,$\sigma(2)=3$,$\sigma(3)=1$
という写像である.この関係が縦の並びで正しく表されていればよいので,これを
$\sigma=\left(\begin{array}{ccc}2&3&1\\ 3&1&2\end{array}\right)$,
$\sigma=\left(\begin{array}{ccc}3&1&2\\ 1&2&3\end{array}\right)$
などと書いてもよい.
$4$ 次の置換
$\sigma=\left(\begin{array}{cccc}1&2&3&4\\4&3&1&2\end{array}\right)$ と同じものはどれか?
$\sigma_1=\left(\begin{array}{cccc}4&3&1&2\\1&2&3&4\end{array}\right)$
$\sigma_2=\left(\begin{array}{cccc}4&3&1&2\\2&1&4&3\end{array}\right)$
$\sigma_3=\left(\begin{array}{cccc}2&4&1&3\\3&2&4&1\end{array}\right)$
$\sigma_4=\left(\begin{array}{cccc}4&2&3&1\\2&3&1&4\end{array}\right)$
$\sigma_2$,$\sigma_3$,$\sigma_4$
二つの置換 $\sigma$,$\tau$ の
積 $\sigma\tau$ は合成写像 $\sigma\circ\tau$ として定義される.異なる次数の積は定義されない.また,
逆元 $\sigma^{-1}$,$\tau^{-1}$ はそれぞれの逆写像である.
$3$ 次の置換
$\sigma=\left(\begin{array}{ccc}1&2&3\\1&3&2\end{array}\right)$,
$\tau=\left(\begin{array}{ccc}1&2&3\\2&3&1\end{array}\right)$ の場合
-
積に関しては
$\sigma\tau(1)=\sigma(2)=3$
$\sigma\tau(2)=\sigma(3)=2$
$\sigma\tau(3)=\sigma(1)=1$
より
$\sigma\tau=\left(\begin{array}{ccc}1&2&3\\3&2&1\end{array}\right)$
となる.
$\sigma\tau$ は写像としては「$\tau$ が先 $\sigma$ が後」なので,$\sigma$ の上段を $\tau$ の下段に揃えて
$\sigma=\left(\begin{array}{ccc}2&3&1\\3&2&1\end{array}\right)$
と書き直して考えると見やすい.
$\tau\sigma$ の場合は「$\sigma$ が先 $\tau$ が後」なので,$\tau$ の上段を $\sigma$ の下段に揃えて
$\sigma=\left(\begin{array}{ccc}1&2&3\\1&3&2\end{array}\right)$,
$\tau=\left(\begin{array}{ccc}1&3&2\\2&1&3\end{array}\right)$
より
$\tau\sigma=\left(\begin{array}{ccc}1&2&3\\2&1&3\end{array}\right)$
となる.
-
逆元に関しては,
$\sigma^{-1}
=\left(\begin{array}{ccc}1&3&2\\1&2&3\end{array}\right)$
と,上段と下段を入れ替えればよい.
$\sigma(i)$ を $i$ に戻すのが逆写像
$\sigma^{-1}$ だからである.
同様に
$\tau^{-1}
=\left(\begin{array}{ccc}2&3&1\\1&2&3\end{array}\right)$
である.できるだけ
$\sigma^{-1}
=\left(\begin{array}{ccc}1&2&3\\1&3&2\end{array}\right)$,
$\tau^{-1}
=\left(\begin{array}{ccc}1&2&3\\3&1&2\end{array}\right)$
と,上段が$1\ 2\ 3$の順になるようそれぞれ書き直しておくほうがよいだろう.
置換の符号
置換 $\sigma$ の
転倒数とは
$i < j $ かつ $\sigma(i) > \sigma(j)$
を満たす組 $(i,j)$ の個数のことをいい,
転倒数が偶数である置換を
偶置換,奇数である置換を
奇置換という.
置換 $\sigma$ の
符号 $\mathrm{sign}(\sigma)$ は
$\mathrm{sign}(\sigma)=\left\{\begin{array}{ll}1&\mbox{($\sigma$ が偶置換のとき)}\\-1&\mbox{($\sigma$ が奇置換のとき)}\end{array}\right.$
で定義される.
-
$3$ 次の置換 $\sigma=\left(\begin{array}{ccc}1&2&3\\3&1&2\end{array}\right)$
の場合,
$\sigma(1) > \sigma(2)$,$\sigma(1) > \sigma(3)$ と
なっており,転倒数は $2$ である.
すなわち
$\sigma=\left(\begin{array}{ccc}1&2&*\\3&1&*\end{array}\right)$,
$\sigma=\left(\begin{array}{ccc}1&*&3\\3&*&2\end{array}\right)$
のように,上段と下段で大小関係が
逆転している組を数えるのである.
よって $\sigma$ は偶置換であるから,その符号は
$\mathrm{sign}(\sigma)=1$.
-
$4$ 次の置換 $\tau=\left(\begin{array}{cccc}1&2&3&4\\3&1&4&2\end{array}\right)$ の場合
$\tau=\left(\begin{array}{cccc}1&2&*&*\\3&1&*&*\end{array}\right)$
$\tau=\left(\begin{array}{cccc}1&*&*&4\\3&*&*&2\end{array}\right)$
$\tau=\left(\begin{array}{cccc}*&*&3&4\\*&*&4&2\end{array}\right)$
と,$3$ 組で転倒しており.転倒数は $3$,$\tau$ は奇置換であるからその符号は $\mathrm{sign}(\tau)=-1$ である.
-
二つの数字のみを入れ替える置換を互換といい,$i$ と $j$ を入れ替える互換を $(\,i\ j\,)$ と表す.例えば $3$ 次の互換の場合
$(\,1\ 3\,)=\left(\begin{array}{ccc}1&2&3\\ 3&2&1\end{array}\right)$
などである.
任意の置換は,例えば
$\left(\begin{array}{ccc}1&2&3\\ 2&3&1\end{array}\right)=(\,1\ 2\,)(\,1\ 3\,)$
のように
いくつかの互換の積で表されるが,
偶置換は偶数個の互換の積で,奇置換は奇数個の互換の積で表される.
このことを確かめるには,互換の転倒数が常に奇数になること,従って互換を掛けるごとに転倒数は奇数個変化することを観察してみるとよい.
-
置換の符号の判定は,場合によっては「いくつの互換の積で表されるか」を見たほうが楽なこともある.例えば,$5$ 次の置換
$\left(\begin{array}{ccccc}1&2&3&4&5\\ 5&3&2&4&1\end{array}\right)$
は,$1$ と$5$,および $2$ と $3$ の入れ替え,すなわち $(\,2\ 3\,)(\,1\ 5\,)$ と偶数個の互換の積で表されるから偶置換である(転倒数は$8$).
対称群
すべての $n$ 次の置換からなる集合を $n$ 次の
対称群といい,$S_n$ で表す.
-
$2$ 次の対称群 $S_2$ は次の $2$ 個の置換からなる集合である:
$\sigma_0=\left(\begin{array}{cc}1&2\\1&2\end{array}\right)$,
$\sigma_1=\left(\begin{array}{cc}1&2\\2&1\end{array}\right)$
$\sigma_0$ は偶置換,$\sigma_1$ は奇置換である.
-
$3$ 次の対称群 $S_3$ は次の $6$ 個の置換からなる集合である:
$\sigma_0=\left(\begin{array}{ccc}1&2&3\\1&2&3\end{array}\right)$
$\sigma_1=\left(\begin{array}{ccc}1&2&3\\1&3&2\end{array}\right)$
$\sigma_2=\left(\begin{array}{ccc}1&2&3\\2&3&1\end{array}\right)$
$\sigma_3=\left(\begin{array}{ccc}1&2&3\\2&1&3\end{array}\right)$
$\sigma_4=\left(\begin{array}{ccc}1&2&3\\3&1&2\end{array}\right)$
$\sigma_5=\left(\begin{array}{ccc}1&2&3\\3&2&1\end{array}\right)$
$\sigma_0,\sigma_2,\sigma_4$は偶置換,$\sigma_1,\sigma_3,\sigma_5$は奇置換である.
-
$n$ 次の置換とは,要するに $n$ 個の数字の並べ替えであるから,それらすべてを集めた $S_n$ は $n!$ 個の置換からなる.
$x_1,x_2,\ldots,x_n$ を変数とする式(多項式など) $f(x_1,x_2,\ldots,x_n)$ が与えられたとき,この式の変数を互いに入れ替えたものすべての和
$\displaystyle \sum_{\sigma\in S_n}f(x_{\sigma(1)},x_{\sigma(2)},\ldots,x_{\sigma(n)})$
を考えることがしばしばある.置換の符号も考慮した
$\displaystyle \sum_{\sigma\in S_n}\mathrm{sign}(\sigma)f(x_{\sigma(1)},x_{\sigma(2)},\ldots,x_{\sigma(n)})$
という操作もよく行われる.
-
$2$ 変数の場合は
$\displaystyle \sum_{\sigma\in S_2}f(x_{\sigma(1)},x_{\sigma(2)})=f(x_1,x_2)+f(x_2,x_1)$
である.また,
$\left(\begin{array}{cc}1&2\\1&2\end{array}\right)$ は偶置換,
$\left(\begin{array}{cc}1&2\\2&1\end{array}\right)$ は奇置換だから
$\displaystyle \sum_{\sigma\in S_2}\mathrm{sign}(\sigma)f(x_{\sigma(1)},x_{\sigma(2)})=f(x_1,x_2)-f(x_2,x_1)$
である.
-
$3$ 変数の場合は
$\displaystyle \sum_{\sigma\in S_3}f(x_{\sigma(1)},x_{\sigma(2)},x_{\sigma(3)})\\
\hspace{30pt}=f(x_1,x_2,x_3)+f(x_1,x_3,x_2)\\
\hspace{40pt}+f(x_2,x_3,x_1)+f(x_2,x_1,x_3)\\
\hspace{40pt}+f(x_3,x_1,x_2)+f(x_3,x_2,x_1)$
であり
$\left(\begin{array}{ccc}1&2&3\\1&2&3\end{array}\right)$,
$\left(\begin{array}{ccc}1&2&3\\2&3&1\end{array}\right)$,
$\left(\begin{array}{ccc}1&2&3\\3&1&2\end{array}\right)$
は偶置換
$\left(\begin{array}{ccc}1&2&3\\1&3&2\end{array}\right)$,
$\left(\begin{array}{ccc}1&2&3\\2&1&3\end{array}\right)$,
$\left(\begin{array}{ccc}1&2&3\\3&2&1\end{array}\right)$
は奇置換だから
$\displaystyle \sum_{\sigma\in S_3}\mathrm{sign}(\sigma)f(x_{\sigma(1)},x_{\sigma(2)},x_{\sigma(3)})\\
\hspace{30pt}=f(x_1,x_2,x_3)-f(x_1,x_3,x_2)\\
\hspace{40pt}+f(x_2,x_3,x_1)-f(x_2,x_1,x_3)\\
\hspace{40pt}+f(x_3,x_1,x_2)-f(x_3,x_2,x_1)$
である.
-
例えば,$f(x_1,x_2,x_3)=x_1+2x_2+3x_3$ とすると
$\displaystyle \sum_{\sigma\in S_3}(x_{\sigma(1)}+2x_{\sigma(2)}+3x_{\sigma(3)})\\
\hspace{20pt}=(x_1+2x_2+3x_3)+(x_1+2x_3+3x_2)\\
\hspace{30pt}+(x_2+2x_3+3x_1)+(x_2+2x_1+3x_3)\\
\hspace{30pt}+(x_3+2x_1+3x_2)+(x_3+2x_2+3x_1)\\
\hspace{20pt}=12(x_1+x_2+x_3)$
$\displaystyle \sum_{\sigma\in S_3}\mathrm{sign}(\sigma)(x_{\sigma(1)}+2x_{\sigma(2)}+3x_{\sigma(3)})\\
\hspace{20pt}=(x_1+2x_2+3x_3)-(x_1+2x_3+3x_2)\\
\hspace{30pt}+(x_2+2x_3+3x_1)-(x_2+2x_1+3x_3)\\
\hspace{30pt}+(x_3+2x_1+3x_2)-(x_3+2x_2+3x_1)\\
\hspace{20pt}=0$
となる.
$n$ 次の置換とは,$n$ 個の対象を並べ替える操作である.その対象とは,一般的な議論においては,ここで見ているように $\{\,1,2,\ldots,n\,\}$ という自然数の組であるが,実際は $n$ 個の異なるものであれば何でもよい.例えば $3$ 次の対称群 $S_3$ の $6$ 個の元を
$\left(\begin{array}{ccc}a&b&c\\a&b&c\end{array}\right)$
$\left(\begin{array}{ccc}a&b&c\\a&c&b\end{array}\right)$
$\left(\begin{array}{ccc}a&b&c\\b&c&a\end{array}\right)$
$\left(\begin{array}{ccc}a&b&c\\b&a&c\end{array}\right)$
$\left(\begin{array}{ccc}a&b&c\\c&a&b\end{array}\right)$
$\left(\begin{array}{ccc}a&b&c\\c&b&a\end{array}\right)$
などと表してもよく,$\{\,1,2,3\,\}$ の並べ替えでなければならないということはない(もちろん,符号の決定などのため $a < b < c$ といった順序は設定しておく必要はあるが).
従って,あまりお目にかかることはないが,仮に
$\displaystyle \sum_{\sigma\in S_3}\{\sigma(a)\sigma(b)+\sigma(c)\}$
というような式に出くわしたとしても,これは
$\displaystyle \sum_{\sigma\in S_3}\{\sigma(a)\sigma(b)+\sigma(c)\}\\
\hspace{50pt}=(ab+c)+(ac+b)\\
\hspace{60pt}+(bc+a)+(ba+c)\\
\hspace{60pt}+(ca+b)+(cb+a)$
と自然に解釈できるのである.
表記法はできるだけ慣習に従うのがよいが,場面に応じてある程度柔軟に対応することも必要である.
行列式
$n$ を $2$ 以上の自然数とするとき,実 $n$ 次正方行列 $A=(a_{ij})$ の行列式 $\det{A}$ は
$\displaystyle \det{A}=\sum_{\sigma\in S_n}\mathrm{sgn}(\sigma)a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{n\sigma(n)}$
により定義される.
もちろん $|A|$ という表記も用いられる.
成分を表記するときはやはり
$\det{A}=\left|\begin{array}{cccc}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\\\end{array}\right|$
と書かれる.
$A$ を
$\mathbf{a}_i=\left(\begin{array}{c}a_{1i}\\a_{2i}\\\vdots \\ a_{ni}\\\end{array}\right)$ $(i=1,2,\ldots,n)$
という $n$ 本のベクトルを並べたものと見て
$A=(\,\mathbf{a}_1\ \mathbf{a}_2\ \cdots\ \mathbf{a}_n\,)$
と表すことがしばしばあるが,その場合は行列式も
$\det{A}=\big|\,\mathbf{a}_1\ \mathbf{a}_2\ \cdots\ \mathbf{a}_n\,\big|$
と表わされる.
-
$S_2$ は
二つの置換
$\sigma_0=\left(\begin{array}{cc}1&2\\1&2\end{array}\right)$,
$\sigma_1=\left(\begin{array}{cc}1&2\\2&1\end{array}\right)$
からなる集合であり,
$\mathrm{sign}(\sigma_0)=1$,
$\mathrm{sign}(\sigma_1)=-1$ だから,$2$ 次の行列式は
$\left|\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\right|
=
a_{1\sigma_0(1)}a_{2\sigma_0(2)}
-a_{1\sigma_1(1)}a_{2\sigma_1(2)}\\[1mm]
\hspace{45pt}=
a_{11}a_{22}-a_{12}a_{21}
$
となり,確かに既に見た定義と一致している.
-
$3$ 次の行列式についても同様であるが,特にこのサイズで添え字の「並べ替え」と符号の対応の様子を観察しておきたい:
対称群 $S_n$ は $n!$ 個の置換からなる集合であるから,次数 $n$ が大きくなると行列式を上の定義通りに計算することは現実的でなくなってくる.
一般的な計算法は次講で詳しく見ることにして,今回は第 $1$ 行が $(1,1)$ 成分を除いてすべて $0$ という,特別な形の行列式の計算の様子を観察しておこう.
例えば $3$ 次の場合は
$
\left|\begin{array}{ccc}a_{11}&0&0\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{array}\right|
=
a_{11}a_{22}a_{33}
-a_{11}a_{23}a_{32}\\
\hspace{65pt}=
a_{11}\left|\begin{array}{cc}a_{22}&a_{23}\\a_{32}&a_{33}\end{array}\right|
$
となっている.$4$ 次の場合も,定義式と見比べて
$
\left|\begin{array}{cccc}a_{11}&0&0&0\\a_{21}&a_{22}&a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41}&a_{42}&a_{43}&a_{44}\\\end{array}\right|
=
a_{11}\left|\begin{array}{cc}a_{22}&a_{23}&a_{24}\\a_{32}&a_{33}&a_{34}\\a_{42}&a_{43}&a_{44}\end{array}\right|
$
が成り立つことがわかる
詳しく!.
真面目に符号を確認しながら各項を書き出すと,確かに
$
\left|\begin{array}{cccc}a_{11}&0&0&0\\a_{21}&a_{22}&a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41}&a_{42}&a_{43}&a_{44}\end{array}\right|\\[3mm]
\hspace{30pt}=a_{11}a_{22}a_{33}a_{44}
-a_{11}a_{22}a_{34}a_{43}\\
\hspace{50pt}+a_{11}a_{23}a_{34}a_{42}
-a_{11}a_{23}a_{32}a_{44}\\
\hspace{50pt}+a_{11}a_{24}a_{32}a_{43}
-a_{11}a_{24}a_{33}a_{42}\\[1mm]
\hspace{30pt}=a_{11}(a_{22}a_{33}a_{44}
-a_{22}a_{34}a_{43}\\
\hspace{65pt}+a_{23}a_{34}a_{42}
-a_{23}a_{32}a_{44}\\
\hspace{75pt}+a_{24}a_{32}a_{43}
-a_{24}a_{33}a_{42})\\[1mm]
\hspace{30pt}
=
a_{11}\left|\begin{array}{cc}a_{22}&a_{23}&a_{24}\\a_{32}&a_{33}&a_{34}\\a_{42}&a_{43}&a_{44}\end{array}\right|
$
となっている.第 $1$ 行の $0\ 0\ 0$ の並びのおかげでこれで済んでいるが,
一般の $4$ 次の行列式を定義通りに計算しようとすると $4!=24$ 個の項を書き出す羽目になる.
$5$ 次だと $5!=120$ 個である.
このように,行列式の計算は次数が大きくなると計算量が膨大になるという問題が出てくるので,次講で見るように,基本的には行列式の一般的性質を利用して「次数を落として」計算する方針が採られる.
同様のことが $5$ 次以上でも成り立つことは,これらの様子を踏まえて定義式を再度見ることで確認できるであろう.