$2$ 次の直交行列 実行列 $T$ が直交行列であるとは
${}^tTT=T^tT=E$
が成り立つことをいうのであった.
特に,$2$ 次の直交行列は
$\left(\begin{array}{cc}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right)$ または $\left(\begin{array}{cc}\cos\theta&\sin\theta\\\sin\theta&-\cos\theta\end{array}\right),\quad \theta\in(-\pi,\pi]$
という形で表される
詳しく!.
$T=\left(\begin{array}{cc}a&b\\c&d\end{array}\right)$ とおくと
${}^tTT=\left(\begin{array}{cc}a&c\\b&d\end{array}\right)\left(\begin{array}{cc}a&b\\c&d\end{array}\right)=\left(\begin{array}{cc}a^2+c^2&ab+cd\\ab+cd&b^2+d^2\end{array}\right)$
となるから,$T$ が直交行列ならば
$\left\{\begin{array}{l}a^2+c^2=1\\ab+cd=0\\b^2+d^2=1\end{array}\right.$
が成り立つ.第1式と第3式より
$a=\cos\theta,\ c=\sin\theta\\
b=\cos\varphi,\ d=\sin\varphi$
を満たす $\theta,\varphi\in(-\pi,\pi]$ が存在するが,このとき第2式より
$\cos\theta\cos\varphi+\sin\theta\sin\varphi=0$
従って三角関数の加法定理により $\cos(\theta-\varphi)=0$ となり,$\theta-\varphi\in(-2\pi,2\pi)$ から $\theta-\varphi=\pm\dfrac{\pi}{2},\pm\dfrac{3}{2}\pi$ とわかる.よって,$\theta-\varphi=-\dfrac{\pi}{2},\dfrac{3}{2}\pi$ なら
$\cos\varphi=-\sin\theta,\quad \sin\varphi=\cos\theta$
であるから
$T=\left(\begin{array}{cc}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right)$
$\theta-\varphi=\dfrac{\pi}{2},-\dfrac{3}{2}\pi$ なら
$\cos\varphi=\sin\theta,\quad \sin\varphi=-\cos\theta$
であるから
$T=\left(\begin{array}{cc}\cos\theta&\sin\theta\\\sin\theta&-\cos\theta\end{array}\right)$
となる.
$xy$ 平面において,前者は原点を中心とした角 $\theta$ の回転移動を,後者は直線 $y=\big(\tan\frac{\theta}{2}\big)\,x$ ($\theta=\pi$ のときは $y$ 軸) に関する対称移動を表す
詳しく!.
-
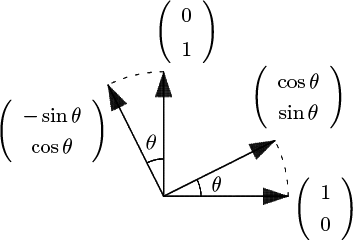
$\mathbf{R}^2$ の標準基底 $\left\{\,\left(\begin{array}{c}1\\0\end{array}\right),\left(\begin{array}{c}0\\1\end{array}\right)\,\right\}$ は
$\left(\begin{array}{cc}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right)\left(\begin{array}{c}1\\0\end{array}\right)=\left(\begin{array}{c}\cos\theta\\\sin\theta\end{array}\right)$
$\left(\begin{array}{cc}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right)\left(\begin{array}{c}0\\1\end{array}\right)=\left(\begin{array}{c}-\sin\theta\\\cos\theta\end{array}\right)$
により $\left\{\,\left(\begin{array}{c}\cos\theta\\\sin\theta\end{array}\right),\left(\begin{array}{c}-\sin\theta\\\cos\theta\end{array}\right)\,\right\}$ に移される.この様子を図で観察すると,この変換が確かに角 $\theta$ の回転を表していることがわかるであろう.
-
まず,$\theta=\pi$ のときは
$\left(\begin{array}{cc}\cos\theta&\sin\theta\\\sin\theta&-\cos\theta\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{cc}-1&0\\0&1\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}-x\\y\end{array}\right)$
より,この変換は確かに $y$ 軸に関する対称移動を表している.$\theta\neq\pi$ のときは,$m=\tan\frac{\theta}{2}$ とおくと
$\cos\theta=\dfrac{1-m^2}{1+m^2},\quad \sin\theta=\dfrac{2m}{1+m^2}$
が成り立つ本当に?
$m=\tan\frac{\theta}{2}$ のとき
$\cos^2\dfrac{\theta}{2}=\dfrac{1}{1+\tan^2\frac{\theta}{2}}=\dfrac{1}{1+m^2}$
より
$\cos\theta=2\cos^2\dfrac{\theta}{2}-1=\dfrac{2}{1+m^2}-1=\dfrac{1-m^2}{1+m^2}$
また,$m\neq \pm1$ に注意して
$\tan\theta=\dfrac{2\tan\frac{\theta}{2}}{1-\tan^2\frac{\theta}{2}}=\dfrac{2m}{1-m^2}$
だから
$\sin\theta=\tan\theta\cos\theta=\dfrac{2m}{1-m^2}\cdot\dfrac{1-m^2}{1+m^2}=\dfrac{2m}{1+m^2}$
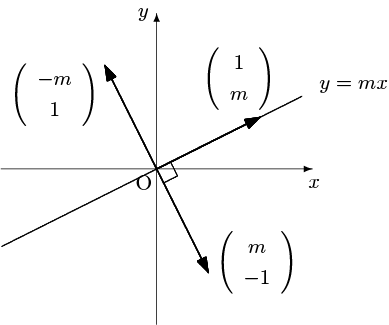
$\left(\begin{array}{cc}\cos\theta&\sin\theta\\\sin\theta&-\cos\theta\end{array}\right)=\dfrac{1}{1+m^2}\left(\begin{array}{cc}1-m^2&2m\\2m&1-m^2\end{array}\right)$
となるが,この行列は
$\dfrac{1}{1+m^2}\left(\begin{array}{cc}1-m^2&2m\\2m&1-m^2\end{array}\right)\left(\begin{array}{c}1\\m\end{array}\right)=\left(\begin{array}{c}1\\m\end{array}\right)$
$\dfrac{1}{1+m^2}\left(\begin{array}{cc}1-m^2&2m\\2m&1-m^2\end{array}\right)\left(\begin{array}{c}m\\-1\end{array}\right)=\left(\begin{array}{c}-m\\1\end{array}\right)$
よりベクトル $\left(\begin{array}{c}1\\m\end{array}\right)$ を動かさず,それと垂直なベクトル $\left(\begin{array}{c}m\\-1\end{array}\right)$ を反転させる.このことはこの変換が直線 $y=mx$ に関する対称移動を表すことを意味する.
直交行列 $A=\dfrac{1}{2}\left(\begin{array}{c}1&-\sqrt{3}\\\sqrt{3}&1\end{array}\right)$ および $B=\dfrac{1}{13}\left(\begin{array}{c}5&12\\12&-5\end{array}\right)$ が $xy$ 平面においてどのような点の移動を表すかそれぞれ調べよう.各成分の符号に注意すると,$A$ は回転を表し,$B$ は対称移動を表すことがわかる.
座標変換と基底の変換
前節では $\mathbf{R}^2$ のベクトルと $xy$ 平面上の点とを同一視するということを断りなく行ったが,ここでこのことについてきちんと考えておこう.
例えば,$\mathbf{R}^2$ のベクトル $\left(\begin{array}{c}2\\3\end{array}\right)$ を $xy$ 平面上の点 $(2,3)$ と同一視するのは自然なことだと思われるが,このことを基底をはっきり意識して
$\left(\begin{array}{c}2\\3\end{array}\right)=2\mathbf{e}_1+3\mathbf{e}_2\quad \leftrightarrow\quad (2,3)$
と表すことにする.ここで,$\{\mathbf{e}_1,\mathbf{e}_2\}=\left\{\,\left(\begin{array}{c}1\\0\end{array}\right),\left(\begin{array}{c}0\\1\end{array}\right)\,\right\}$ は $\mathbf{R}^2$ の標準基底である.何が言いたいのかというと,ベクトルを座標平面(座標空間)上の点として表すというのは,そのベクトルを基底の線型結合として表すことであり,従ってその表し方は基底に依存するということである.もし基底を $\{\mathbf{a}_1,\mathbf{a}_2\}=\left\{\,\left(\begin{array}{c}-1\\2\end{array}\right),\left(\begin{array}{c}3\\1\end{array}\right)\,\right\}$ ととったならば
$\left(\begin{array}{c}2\\3\end{array}\right)=\mathbf{a}_1+\mathbf{a}_2\quad \leftrightarrow\quad (1,1)$
という対応になり,この場合はベクトル $\left(\begin{array}{c}2\\3\end{array}\right)$ は点 $(1,1)$ と同一視されることになる.
ベクトル $\left(\begin{array}{c}2\\3\end{array}\right)$ を点 $(1,1)$ と同一視するというのは奇妙なことに感じられるだろうし,なぜわざわざそんな基底をとるのか,いつも標準基底をとればいいではないかという気持ちももっともであるが,$\mathbf{R}^3$ の部分空間
$W=\left\{\left.\,\left(\begin{array}{c}x\\y\\z\end{array}\right)\,\right|\,x+y+z=0\,\right\}$
なども考えてみるとよい.この $W$ は $2$ 次元部分空間であり,$xyz$ 空間の中の平面を表すから,$W$ のベクトルは $xy$ 平面上の点として表せるはずである.実際,$W$ の基底としては例えば $\left\{\,\left(\begin{array}{c}1\\-1\\0\end{array}\right),\left(\begin{array}{c}0\\1\\-1\end{array}\right)\,\right\}$ がとれるから,これを用いて $W$ のベクトル $\left(\begin{array}{c}2\\1\\-3\end{array}\right)$ を表すと
$\left(\begin{array}{c}2\\1\\-3\end{array}\right)=2\left(\begin{array}{c}1\\-1\\0\end{array}\right)+3\left(\begin{array}{c}0\\1\\-1\end{array}\right)$
となり,$xy$ 平面上の点 $(2,3)$ として表せる.また,基底として $\left\{\,\left(\begin{array}{c}1\\0\\-1\end{array}\right),\left(\begin{array}{c}1\\1\\-2\end{array}\right)\,\right\}$ をとったならば
$\left(\begin{array}{c}2\\1\\-3\end{array}\right)=\left(\begin{array}{c}1\\0\\-1\end{array}\right)+\left(\begin{array}{c}1\\1\\-2\end{array}\right)$
となり,この場合は点 $(1,1)$ として表すことになる.これらの対応
$\left(\begin{array}{c}2\\1\\-3\end{array}\right)=2\left(\begin{array}{c}1\\-1\\0\end{array}\right)+3\left(\begin{array}{c}0\\1\\-1\end{array}\right)\quad\leftrightarrow\quad (2,3)$
$\left(\begin{array}{c}2\\1\\-3\end{array}\right)=\left(\begin{array}{c}1\\0\\-1\end{array}\right)+\left(\begin{array}{c}1\\1\\-2\end{array}\right)\quad\leftrightarrow\quad (1,1)$
を比較してどちらがより自然な表し方であるとは一概には言えまい.
$\mathbf{R}^2$ のベクトルを $xy$ 平面上の点と,あるいは $\mathbf{R}^3$ のベクトルを $xyz$ 空間上の点とみなす場合は,暗黙に標準基底をとっていることが多いが,他の基底のとり方もあり得ることは意識しておくべきである.標語的にまとめると
ベクトル空間の基底を決定することは,各ベクトルの「座標」を決定することである
ということができよう.
上記を踏まえて,直交行列 $T$ によるベクトルの変換
$\left(\begin{array}{c}x'\\y'\end{array}\right)=T\left(\begin{array}{c}x\\y\end{array}\right)$
を考える.前節のように,これは点 $(x,y)$ が点 $(x',y')$ に移動したと考えてよいのだが,これを( $T^{-1}={}^tT$ に注意して)
${}^tT\left(\begin{array}{c}x'\\y'\end{array}\right)=\left(\begin{array}{c}x\\y\end{array}\right)$
と書き直し,さらに $(\mathbf{u}_1\ \mathbf{u}_2)=(\mathbf{e}_1\ \mathbf{e}){}^tT$ とおくと
$(\mathbf{u}_1\ \mathbf{u}_2)\left(\begin{array}{c}x'\\y'\end{array}\right)=(\mathbf{e}_1\ \mathbf{e})\left(\begin{array}{c}x\\y\end{array}\right)$
すなわち
$x'\mathbf{u}_1+y'\mathbf{u}_2=x\mathbf{e}_1+y\mathbf{e}_2$
という関係が得られる.点は動いていないが,$T$ (の逆行列)によって基底が変換されたためにその座標が $(x,y)$ から $(x',y')$ に変化したのだという見方である.例えば,回転を表す行列 $\left(\begin{array}{c}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{array}\right)$ は,点を $\theta$ だけ回転させるとも言えるし,点は動かさずに基底を(すなわち座標軸を) $-\theta$ だけ回転させるのだと言うこともできるのである.
直交行列による変換に限らず,一般に正則行列について同様のことが言える.すなわち,正則行列 $A$ による
$\left(\begin{array}{c}x'\\y'\end{array}\right)=A\left(\begin{array}{c}x\\y\end{array}\right)$
という変換が与えられたとき
$(\mathbf{u}_1\ \mathbf{u}_2)=(\mathbf{e}_1\ \mathbf{e}_2)A^{-1}$
と基底のほうを変換することにより
$x'\mathbf{u}_1+y'\mathbf{u}_2=x\mathbf{e}_1+y\mathbf{e}_2$
という関係が得られる.
ここで,$\{\mathbf{a}_1,\ldots,\mathbf{a}_n\}$ が $\mathbf{R}^n$ の基底であることは行列 $(\mathbf{a}_1 \cdots\ \mathbf{a}_n)$ が正則であることと同値であったから,$P$ が正則行列ならば
$(\mathbf{b}_1\ \cdots\ \mathbf{b}_n)=(\mathbf{a}_1 \cdots\ \mathbf{a}_n)P$
により得られる組 $\{\mathbf{b}_1,\ldots,\mathbf{b}_n\}$ もやはり $\mathbf{R}^n$ の基底であることに注意しよう.特に,$\mathbf{R}^n$ の正規直交基底(内積はドット積)を直交行列で変換して得られる組はまた正規直交基底である.
なぜなら,前講で見たように,直交行列は正規直交基底を並べた形をしており,直交行列どうしの積はまた直交行列だからである.
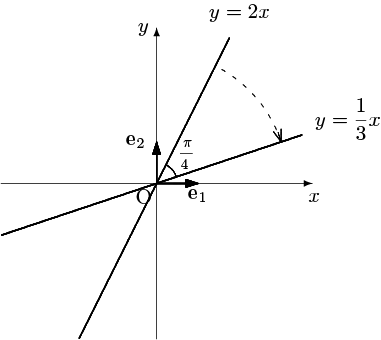
$xy$ 平面における直線 $y=2x$ が
$\left\{\begin{array}{l}x'=\dfrac{x+y}{\sqrt{2}}\\y'=\dfrac{-x+y}{\sqrt{2}}\end{array}\right.$
という変換によりどのように移されるか調べよう.与えられた関係は
$\left(\begin{array}{c}x'\\y'\end{array}\right)=\dfrac{1}{\sqrt{2}}\left(\begin{array}{cc}1&1\\-1&1\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)$
と書けるから,$T=\dfrac{1}{\sqrt{2}}\left(\begin{array}{cc}1&1\\-1&1\end{array}\right)$ とおく.
また,直線 $y=2x$ 上の任意の点は $(t,2t),\ t\in\mathbf{R}$ と表わせるから,$\mathbf{R}^2$ の標準基底 $\{\mathbf{e}_1,\mathbf{e}_2\}$ により
$\left(\begin{array}{c}t\\2t\end{array}\right)
=t\mathbf{e}_1+2t\mathbf{e}_2\quad\leftrightarrow\quad(t,2t)$
と自然に同一視できる.
-
ベクトル $\left(\begin{array}{c}t\\2t\end{array}\right)$ は $T$ により
$T\left(\begin{array}{c}t\\2t\end{array}\right)=\dfrac{t}{\sqrt{2}}\left(\begin{array}{c}3\\1\end{array}\right)
$
と変換され,得られたベクトルはもちろん
$\dfrac{1}{\sqrt{2}}\left(\begin{array}{c}3t\\t\end{array}\right)
=\dfrac{3t}{\sqrt{2}}\mathbf{e}_1+\dfrac{t}{\sqrt{2}}\mathbf{e}_2\quad\leftrightarrow\quad\Big(\dfrac{3t}{\sqrt{2}},\dfrac{t}{\sqrt{2}}\Big)$
と対応する.
よって,$x=\dfrac{3t}{\sqrt{2}},\ y=\dfrac{t}{\sqrt{2}}$ から $t$ を消去することにより $y=\dfrac{x}{3}$ を得る.$T$ は直交行列であり,前節で見たように $xy$ 平面において原点を中心とした角 $-\dfrac{\pi}{4}$ の回転移動を表すから,$T$ によりすべての点が(直線もろとも)回転されたと考えればよい.基底は一貫して標準基底を用いている(すなわち同じ座標系で考えている)ので同じ $x,y$ を用いて表している.
以上は,謂わば「観測者は動かずに直線が動いている」という見方である.
-
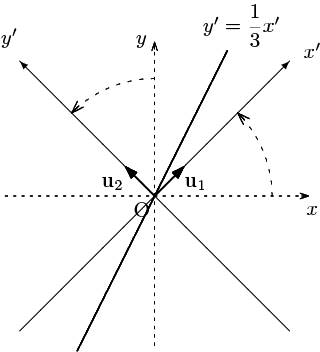
$T$ による基底の変換
$(\mathbf{e}_1\ \mathbf{e}_2)\,{}^tT=\dfrac{1}{\sqrt{2}}
\left(\begin{array}{cc}1&-1\\1&1\end{array}\right)$
により,新しい正規直交基底
$\{\mathbf{u}_1,\mathbf{u}_2\}=\left\{\,\dfrac{1}{\sqrt{2}}\left(\begin{array}{c}1\\1\end{array}\right),\dfrac{1}{\sqrt{2}}\left(\begin{array}{c}-1\\1\end{array}\right)\right\}$
が得られるが,これを用いてベクトル $\left(\begin{array}{c}t\\2t\end{array}\right)$ を表す
$\{\mathbf{u}_1,\mathbf{u}_2,\ldots,\mathbf{u}_n\}$ が正規直交基底ならば任意のベクトル $\mathbf{v}$ は
$\mathbf{v}=(\mathbf{v}\cdot\mathbf{u}_1)\mathbf{u}_1+(\mathbf{v}\cdot\mathbf{u}_2)\mathbf{u}_2+\cdots+(\mathbf{v}\cdot\mathbf{u}_n)\mathbf{u}_n$
と表わせることも思い出そう.
$\left(\begin{array}{c}t\\2t\end{array}\right)
=\dfrac{3t}{\sqrt{2}}\mathbf{u}_1+\dfrac{t}{\sqrt{2}}\mathbf{u}_2\quad\leftrightarrow\quad\Big(\dfrac{3t}{\sqrt{2}},\dfrac{t}{\sqrt{2}}\Big)$
という対応が得られる.
よって,$x'=\dfrac{3t}{\sqrt{2}},\ y'=\dfrac{t}{\sqrt{2}}$ とおいて $t$ を消去することにより $y'=\dfrac{x'}{3}$ を得る.基底(座標系)を取り換えているので $x,y$ ではなく $x',y'$ を用いた.
以上が「直線は動かずに観測者(座標軸)が動いている」という見方である.すなわち,座標軸を $\dfrac{\pi}{4}$ 回転させ新しく $x'$ 軸,$y'$ 軸を設定してもとの直線を表したのである.
二次形式 $n$ 次対称行列 $A$ により
${}^t\mathbf{x}A\mathbf{x}\quad(\mathbf{x}\in\mathbf{R}^n)$
と表わされる式を
二次形式という.成分で表すと
$\displaystyle {}^t\mathbf{x}A\mathbf{x}=\sum_{i=1}^na_{ii}{x_i}^2+2\sum_{i < j}a_{ij}x_ix_j$
という形になる(すべて2次の項なので「二次形式」である)が,適当な変数変換を行うことにより
$\displaystyle {}^t\mathbf{x}A\mathbf{x}=\sum_{k=1}^n\alpha_k{x_k'}^2$
と表わすことができる
詳しく!.
前講で見たように,対称行列 $A$ は適当な直交行列 $T$ と実対角行列 $D$ により $A={}^tTDT$ と表わすことができる
どちらかというと $A=TD\,{}^tT$ と書いたほうがよいのだが,今回は変数変換に注目したいのでこのように書く.
から,このとき
${}^t\mathbf{x}A\mathbf{x}={}^t\mathbf{x}{}^tT\,D\,T\mathbf{x}={}^t(T\mathbf{x})\,D\,T\mathbf{x}$
となり,そこで,$\mathbf{x}'=T\mathbf{x}$ とおけば上記の表現が得られる.実際
$D=\left(\begin{array}{cccc}\alpha_1&&&\\&\alpha_2&&\\&&\ddots&\\&&&\alpha_n\end{array}\right),\quad \mathbf{x}'=\left(\begin{array}{c}x_1'\\x_2'\\\vdots\\x_n'\end{array}\right)$
とすると
${}^t\mathbf{x}A\mathbf{x}={}^t\mathbf{x}'D\mathbf{x}'\\
\hspace{23pt}=\left(\begin{array}{cccc}x_1'&x_2'&\cdots&x_n'\end{array}\right)
\left(\begin{array}{cccc}\alpha_1&&&\\&\alpha_2&&\\&&\ddots&\\&&&\alpha_n\end{array}\right)\left(\begin{array}{c}x_1'\\x_2'\\\vdots\\x_n'\end{array}\right)\\
\hspace{23pt}=\left(\begin{array}{cccc}\alpha_1x_1'&\alpha_2x_2'&\cdots&\alpha_nx_n'\end{array}\right)
\left(\begin{array}{c}x_1'\\x_2'\\\vdots\\x_n'\end{array}\right)\\
\hspace{23pt}=\alpha_1{x_1'}^2+\alpha_2{x_2'}^2+\cdots+\alpha_n{x_n'}^2
$
となる.
二次形式を用いて表される式
$5x^2+6xy+5y^2=8$
が $xy$ 平面上でどのような図形を表すか調べよう.この式は
$\left(\begin{array}{cc}x&y\end{array}\right)\left(\begin{array}{cc}5&3\\3&5\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=8$
と表わすことができるが,ここに現れた対称行列を直交行列を用いて対角化すると
$\left(\begin{array}{cc}5&3\\3&5\end{array}\right)
=\left(\begin{array}{cc}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{array}\right)\left(\begin{array}{cc}2&0\\0&8\end{array}\right)\left(\begin{array}{cc}\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{array}\right)$
となる.そこで
$T=\left(\begin{array}{cc}\frac{1}{\sqrt{2}}&-\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{array}\right)$,
$\left(\begin{array}{c}x'\\y'\end{array}\right)=T\left(\begin{array}{c}x\\y\end{array}\right)$
とおくと
$\left(\begin{array}{cc}x'&y'\end{array}\right)\left(\begin{array}{cc}2&0\\0&8\end{array}\right)\left(\begin{array}{c}x'\\y'\end{array}\right)=8$
となる.
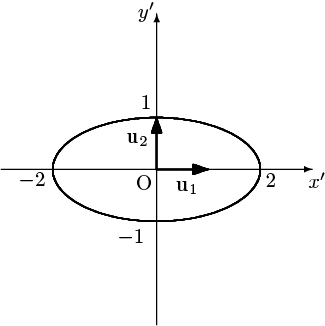
この左辺を計算して $2{x'}^2+8{y'}^2=8$,すなわち
$\dfrac{{x'}^2}{4}+{y'}^2=1$
という形が得られ,これは楕円を表す.
このとき,標準基底 $\{\mathbf{e}_1,\mathbf{e}_2\}$ は
$(\,\mathbf{e}_1\ \mathbf{e}_2\,)\,{}^tT=\left(\begin{array}{cc}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\\-\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}\end{array}\right)$
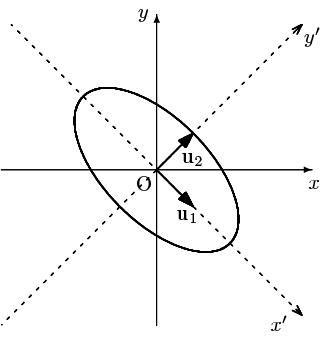
により $\{\mathbf{u}_1,\mathbf{u}_2\}=\left\{\,\dfrac{1}{\sqrt{2}}\left(\begin{array}{c}1\\-1\end{array}\right),\dfrac{1}{\sqrt{2}}\left(\begin{array}{c}1\\1\end{array}\right)\,\right\}$ に変換されたと見ることができ
詳しく!
しつこいようではあるが,ベクトルとその座標に関して,今行っていることをはっきりさせておきたい.
与えられた式 $5x^2+6xy+5y^2=8$ を満たす $xy$ 平面上の点の集合を,$\mathbf{R}^2$ のベクトルの集合
$C=\left\{\,x\mathbf{e}_1+y\mathbf{e}_2\,\left|\,5x^2+6xy+5y^2=8\,\right\}\right.$
と同一視した上で,これを基底 $\{\mathbf{u}_1,\mathbf{u}_2\}$ を用いると
$C=\left\{\,x'\mathbf{u}_1+y'\mathbf{u}_2\,\left|\,\dfrac{{x'}^2}{4}+{y'}^2=1\,\right\}\right.$
と表わすことができ,従って $C$ のベクトルを $x'y'$ 平面上の点として図示ことができたというのが今の状況である.そこで,基底 $\{\mathbf{e}_1,\mathbf{e}_2\}$ と $\{\mathbf{u}_1,\mathbf{u}_2\}$ の関係をみることで改めて $C$ のベクトルを $xy$ 平面上の点として図示しようとしているのである.
その結果が上図であるから,標準基底に(すなわち $xy$ 平面に)戻して表すと下図のようになる: