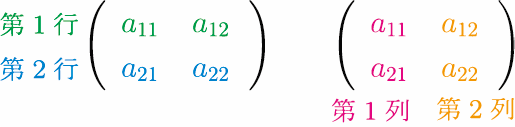第1講 実2次正方行列の演算
行列の記法
$4$ 個の実数 $a_{11}$,$a_{12}$,$a_{21}$,$a_{22}$ を
$\left(\!\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\!\right)$
のように $2$ 行 $2$ 列に配置したものを
実 $2$ 行 $2$ 列行列,
実 $2\times2$ 行列,
実 $2$ 次正方行列などという.
行列は次のように大文字のローマ字で表すことが多い:
$A=\left(\begin{array}{cc}1&2\\5&4\end{array}\right)$,
$B=\left(\begin{array}{cc}3&-4\\1&-2\end{array}\right)$
横の並びを上から第 $1$ 行,第 $2$ 行と呼び,縦の並びを左から第 $1$ 列,第 $2$ 列と呼ぶ.
第 $i$ 行,第 $j$ 列に位置する数 $a_{ij}$ をこの行列の
$(i,j)$ 成分という.特に,行番号と列番号が一致する成分 $a_{11}$ と $a_{22}$ は
対角成分と呼ばれる.
次に与えられる行列 $A$ ~ $D$ について,
| $A=\left(\!\begin{array}{cc}5&4\\-1&1\end{array}\!\right)\quad$ |
$B=\left(\!\begin{array}{cc}4&-3\\-3&4\end{array}\!\right)$ |
| $C=\left(\!\begin{array}{cc}-1&5\\6&-3\end{array}\!\right)\quad$ |
$D=\left(\!\begin{array}{cc}3&-1\\-2&-7\end{array}\!\right)$ |
| $\mathrm{(1)}\ $ |
$(1,2)$ 成分が $(2,1)$ 成分より大きいものはどれか. |
| $\mathrm{(2)}\ $ |
対角成分の和がもっとも大きいものはどれか. |
$\mathrm{(1)}$ $A$ と $D$
$\mathrm{(2)}$ $B$
一般に,成分がすべて実数である行列を実行列という.
虚数の成分をもつ行列,例えば
$\left(\!\begin{array}{cc}1+2i&3\\-4i&2-5i\end{array}\!\right)$
のようなもの含めて,成分が複素数である行列を
複素行列という.
通常,「行列」というときは複素行列を指すのであるが,
本講では当面は実行列しか扱わないので,「行列」は実行列のことだと考えて構わない.
和,スカラー倍,積
実 $2\times 2$ 行列の和とスカラー倍(実数倍)はそれぞれ次で定義される:
$\left(\!\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\!\right)
+\left(\!\begin{array}{cc}b_{11}&b_{12}\\b_{21}&b_{22}\end{array}\!\right)
$$=\left(\!\begin{array}{cc}a_{11}+b_{11}&a_{12}+b_{12}\\a_{21}+b_{21}&a_{22}+b_{22}\end{array}\!\right)$
$k\left(\!\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\!\right)
$$=\left(\!\begin{array}{cc}ka_{11}&ka_{12}\\ka_{21}&ka_{22}\end{array}\!\right)$ ($k\in\mathbf{R}$)
$A=\left(\begin{array}{cc}1&2\\5&4\end{array}\right)$,
$B=\left(\begin{array}{cc}3&-4\\1&-2\end{array}\right)$とすると
$A+B
=\left(\begin{array}{cc}1+3&2+(-4)\\5+1&4+(-2)\end{array}\right)
=\left(\begin{array}{cc}4&-2\\6&2\end{array}\right)$
$2A=\left(\begin{array}{cc}2\times1&2\times2\\2\times5&2\times4\end{array}\right)
=\left(\begin{array}{cc}2&4\\10&8\end{array}\right)$
実数の文字式やベクトルの場合と同様に,$(-1)A$ のことを $-A$ と書く:
$-A=\left(\begin{array}{cc}(-1)\times1&(-1)\times2\\(-1)\times5&(-1)\times4\end{array}\right)
=\left(\begin{array}{cc}-1&-2\\-5&-4\end{array}\right)$
当面は実行列しか扱わないのでスカラーとは実数のことを指す.
複素行列を考える場合はスカラーも複素数となる.
また,積は次で定義される:
$\left(\!\begin{array}{cc}a_{11}&a_{12}\\a_{21}&a_{22}\end{array}\!\right)\left(\!\begin{array}{cc}b_{11}&b_{12}\\b_{21}&b_{22}\end{array}\!\right)
$$=\left(\!\begin{array}{cc}a_{11}b_{11}+a_{12}b_{21}&a_{11}b_{12}+a_{12}b_{22}\\a_{21}b_{11}+a_{22}b_{21}&a_{21}b_{12}+a_{22}b_{22}\end{array}\!\right)$
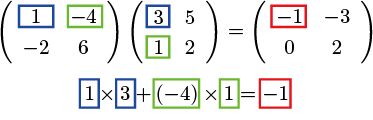
$A=\left(\begin{array}{cc}1&-4\\-2&6\end{array}\right)$,
$B=\left(\begin{array}{cc}3&5\\1&2\end{array}\right)$とすると
| $AB$ | $=$ | $\left(\begin{array}{cc}1&-4\\-2&6\end{array}\right)
\left(\begin{array}{cc}3&5\\1&2\end{array}\right)$ |
| $=$ | $\left(\begin{array}{cc}1\times3+(-4)\times1&1\times5+(-4)\times2\\-2\times3+6\times1&-2\times5+6\times2\end{array}\right)$ |
| $=$ | $\left(\begin{array}{cc}-1&-3\\0&2\end{array}\right)$ |
積に関しては多少の練習が必要であろう.一般のサイズの行列でも同様の計算となるので,$2\times 2$ の場合でしっかり感覚を身につけて欲しい.
また,$AA$ のことを $A^2$ と表すことなども実数の文字式と同様である:
| $A^2$ | $=$ | $\left(\begin{array}{cc}1&-4\\-2&6\end{array}\right)
\left(\begin{array}{cc}1&-4\\-2&6\end{array}\right)$ |
| $=$ | $\left(\begin{array}{cc}9&-28\\-14&44\end{array}\right)$ |
文字式の計算と同様に結合法則,分配法則等を用いてよい
命題1.1
が,
積に関する交換法則は成り立たない
ことに注意せよ
詳しく!.
一般に,行列 $A$,$B$ の積について $AB=BA$ は成り立たない.
例えば,
$A=\left(\begin{array}{cc}1&0\\2&0\end{array}\right)$,
$B=\left(\begin{array}{cc}1&2\\0&0\end{array}\right)$ とすると
$AB=\left(\begin{array}{cc}1&0\\2&0\end{array}\right)\left(\begin{array}{cc}1&2\\0&0\end{array}\right)
=\left(\begin{array}{cc}1&2\\2&4\end{array}\right)$
$BA=\left(\begin{array}{cc}1&2\\0&0\end{array}\right)\left(\begin{array}{cc}1&0\\2&0\end{array}\right)
=\left(\begin{array}{cc}5&0\\0&0\end{array}\right)$
もちろん
たまたま成り立つこともある.例えば,
$C=\left(\begin{array}{cc}1&1\\2&1\end{array}\right)$,
$D=\left(\begin{array}{cc}1&2\\4&1\end{array}\right)$ とすると
$CD=\left(\begin{array}{cc}1&1\\2&1\end{array}\right)\left(\begin{array}{cc}1&2\\4&1\end{array}\right)
=\left(\begin{array}{cc}5&3\\6&5\end{array}\right)$
$DC=\left(\begin{array}{cc}1&2\\4&1\end{array}\right)\left(\begin{array}{cc}1&1\\2&1\end{array}\right)
=\left(\begin{array}{cc}5&3\\6&5\end{array}\right)$
実 $2\times 2$ 行列 $A$,$B$ について,次の「展開公式」は正しいか?
$(A+B)^2=A^2+2AB+B^2$
$(A+B)(A-B)=A^2-B^2$
ともに正しくない.
分配法則を正しく用いると
$(A+B)^2=A^2+AB+BA+B^2$
$(A+B)(A-B)=A^2-AB+BA-B^2$
となり,一般には $AB\neq BA$ だからである.
単位行列と零行列
次の行列はそれぞれ $2$ 次の
単位行列,
零行列と呼ばれる.
$E=\left(\!\begin{array}{cc}1&0\\0&1\end{array}\!\right)$,
$O=\left(\!\begin{array}{cc}0&0\\0&0\end{array}\!\right)$
容易にわかるように,任意の実 $2\times 2$ 行列 $A$ に対して
$AE=EA=A$
$A+O=A$
$AO=OA=O$
|
が成り立つ
詳しく!.
実際,任意の $a,b,c,d\in\mathbf{R}$ に対して
・$\left(\!\begin{array}{cc}a&b\\c&d\end{array}\!\right)
\left(\!\begin{array}{cc}1&0\\0&1\end{array}\!\right)
=
\left(\!\begin{array}{cc}a&b\\c&d\end{array}\!\right)$
$\left(\!\begin{array}{cc}1&0\\0&1\end{array}\!\right)
\left(\!\begin{array}{cc}a&b\\c&d\end{array}\!\right)
=
\left(\!\begin{array}{cc}a&b\\c&d\end{array}\!\right)$
・$\left(\!\begin{array}{cc}a&b\\c&d\end{array}\!\right)
+\left(\!\begin{array}{cc}0&0\\0&0\end{array}\!\right)
=
\left(\!\begin{array}{cc}a&b\\c&d\end{array}\!\right)$
・$\left(\!\begin{array}{cc}a&b\\c&d\end{array}\!\right)
\left(\!\begin{array}{cc}0&0\\0&0\end{array}\!\right)
=\left(\!\begin{array}{cc}0&0\\0&0\end{array}\!\right)$
$\left(\!\begin{array}{cc}0&0\\0&0\end{array}\!\right)
\left(\!\begin{array}{cc}a&b\\c&d\end{array}\!\right)
=
\left(\!\begin{array}{cc}0&0\\0&0\end{array}\!\right)$
となることは直ちに確かめられる.
実 $2\times 2$ 行列 $A$,$2$ 次の単位行列 $E$ について,次の「展開公式」は正しいか?
$(A+E)^2=A^2+2A+E$
$(A+E)(A-E)=A^2-E$
ともに正しい.
$AE=EA=A$ および $E^2=E$ が成り立つからである.
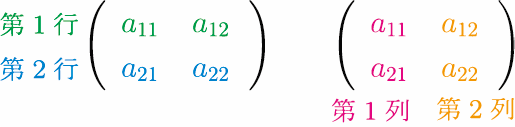 第 $i$ 行,第 $j$ 列に位置する数 $a_{ij}$ をこの行列の $(i,j)$ 成分という.特に,行番号と列番号が一致する成分 $a_{11}$ と $a_{22}$ は 対角成分と呼ばれる.
第 $i$ 行,第 $j$ 列に位置する数 $a_{ij}$ をこの行列の $(i,j)$ 成分という.特に,行番号と列番号が一致する成分 $a_{11}$ と $a_{22}$ は 対角成分と呼ばれる.