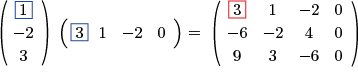第5講 一般の行列の演算,3次の行列式
一般の行列の記法
実 $m\times n$ ($m$ 行 $n$ 列)行列は $mn$ 個の実数を
$
A=\left(\begin{array}{cccc}a_{11}&a_{12}&\cdots&a_{1n}\\
a_{21}&a_{22}&\cdots&a_{2n}\\
\vdots& \vdots&\ddots&\vdots\\a_{m1}&a_{m2}&\cdots&a_{mn}\end{array}\right)
$
のように $m$ 行,$n$ 列に配置したものである.
これを
$A=(a_{ij})\quad(1\le i\le m,\ 1\le j\le n)$
あるいは
$A=(a_{ij})_{1\le i\le m,\ 1\le j\le n}$
などと書く.
サイズが了解されているときや任意であるときは,単に $A=(a_{ij})$ とだけ書くことも多い.
標準的な表記法では,$a_{ij}$ と書いたときの $i$ が行番号,$j$ が列番号であり,これをこの行列の $(i,j)$ 成分という.
$n$ 次正方行列( $n\times n$ 行列)の $a_{11},a_{22},\ldots,a_{nn}$ を対角成分と呼ぶことなども $2\times 2$ の場合と同様である.
$A=(a_{ij})_{1\le i\le 3,\ 1\le j\le 2}$,$a_{ij}=i+j^2$ であれば,これは $3\times 2$ ($3$ 行 $2$ 列) 行列であって
$A=\left(\begin{array}{cc}1+1^2&1+2^2\\2+1^2&2+2^2\\3+1^2&3+2^2\end{array}\right)=\left(\begin{array}{cc}2&5\\3&6\\4&7\end{array}\right)$
一般の行列の演算
$2\times 2$ の場合と同様に,一般の行列の和・スカラー倍は
$(a_{ij})+(b_{ij})=(a_{ij}+b_{ij})$
$k(a_{ij})=(ka_{ij})$
と定義されるが,
サイズが異なる行列どうしの和は定義されない.
例えば,和は
$\left(\begin{array}{cc}3&2\\-1&5\\0&1\end{array}\right)+\left(\begin{array}{cc}-1&4\\6&-4\\1&-3\end{array}\right)=\left(\begin{array}{cc}2&6\\5&1\\1&-2\end{array}\right)$
スカラー倍は
$3\left(\begin{array}{cc}3&2\\-1&5\\0&1\end{array}\right)=\left(\begin{array}{cc}9&6\\-3&15\\0&3\end{array}\right)$
と,$2\times2$ の場合と同様に計算すればよい.サイズが違うものどうしの和
$\left(\begin{array}{cc}3&2\\-1&5\\0&1\end{array}\right)+\left(\begin{array}{ccc}2&5&1\\6&1&-2\end{array}\right)$
のようなものは定義されない.
行列 $A$ と行列 $B$ の積 $AB$ は $A$ の列数と $B$ の行数が等しいときにのみ定義される.
$A=(a_{ij})_{1\le i\le l,\ 1\le j\le m}$ が $l\times m$ 行列
$B=(b_{ij})_{1\le i\le m,\ 1\le j\le n}$ が $m\times n$ 行列
であれば,
その積 $AB$ は
$\displaystyle AB=\left(\sum_{k=1}^ma_{ik}b_{kj}\right)_{1\le i\le l,\ 1\le j\le n}$
と定義され,これは $l\times n$ 行列である.
$2\times 2$ の場合と同様に計算する:
$1$ 列と $1$ 行だと少し戸惑うかもしれないが, やはり同様:
また,$1\times 1$ 行列の括弧は省略することが多い:
$\left(\begin{array}{ccc}1&3&2\end{array}\right)\left(\begin{array}{c}2\\4\\3\end{array}\right)=1\times2+3\times4+2\times3 =20$
次のような積は定義されない:
$\left(\begin{array}{ccc}1&3&0\\1&4&-2\end{array}\right)\left(\begin{array}{cc}4&1\\6&3\end{array}\right)$
左の行列の列数と右の行列の行数が一致しないからである.
和に関する結合法則・交換法則,積に関する結合法則,および分配法則等は成り立つ
命題5.1が,積に関する交換法則はもちろん成り立たない.
転置行列
行列 $A$ の行と列を入れ替えたものを $A$ の
転置行列といい,${}^t\!A$ と表す.
すなわち
$A=(a_{ij})_{1\le i\le m,\ 1\le j\le n}$
ならば
${}^t\!A=(a_{ji})_{1\le j\le n,\ 1\le i\le m}$
である.
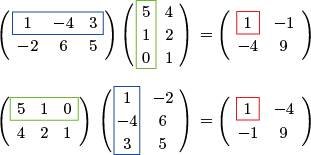
$A=\left(\begin{array}{ccc}7&1&5\\3&0&-1\\-2&1&8\\0&9&2\\\end{array}\right)$ とする.${}^t\!{A}$ はどれか?
$\mathrm{(a)}$
$\left(\begin{array}{cccc}5&-1&8&2\\1&0&1&9\\7&3&-2&0\end{array}\right)\quad$
$\mathrm{(b)}$
$\left(\begin{array}{cccc}0&-2&3&7\\9&1&0&1\\2&8&-1&5\end{array}\right)$
$\mathrm{(c)}$
$\left(\begin{array}{cccc}7&3&-2&0\\1&0&1&9\\5&-1&8&2\end{array}\right)\quad$
$\mathrm{(d)}$
$\left(\begin{array}{cccc}2&8&-1&5\\9&1&0&1\\0&-2&3&7\end{array}\right)$
$\mathrm{(c)}$
転置行列について,
${}^t({}^t\!A)=A$,${}^t(A+B)={}^t\!A+{}^tB$
などが成り立つことは明らかであろう.
また,積 $AB$ が定義できるならば ${}^tB\,{}^t\!A$ も定義できて
${}^t(AB)={}^tB\,{}^t\!A$
が成り立つ
詳しく!.
実際,$A=(a_{ij})_{1\le i\le l,\ 1\le j\le m}$,$B=(b_{ij})_{1\le i\le m,\ 1\le j\le n}$ とすると,$AB$ の $(i,j)$ 成分は
$\displaystyle
\left(\begin{array}{ccc}a_{i1}&\cdots&a_{im}\end{array}\right)
\left(\begin{array}{c}b_{1j}\\\vdots\\ b_{mj}\end{array}\right)
=\sum_{k=1}^ma_{ik}b_{kj}
$
であり,${}^tB\,{}^t\!A$ の $(j,i)$ 成分は
$\displaystyle
\left(\begin{array}{ccc}b_{1j}&\cdots&b_{mj}\end{array}\right)
\left(\begin{array}{c}a_{i1}\\\vdots\\ a_{im}\end{array}\right)
=\sum_{k=1}^mb_{kj}a_{ik}
$
である.
具体例をよく観察すると,成り立つのは当然という気がしてくると思う:
3次の行列式
$3$ 次の行列式は次式で定義される:
$\left|\begin{array}{ccc}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{array}\right|=
\begin{array}{l}
\\[12pt]
a_{11}a_{22}a_{33}-a_{11}a_{23}a_{32}\\
\hspace{10pt}+a_{12}a_{23}a_{31}-a_{12}a_{21}a_{33}\\
\hspace{20pt}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}
\end{array}$
次のように,足す項と引く項に分けると計算し易い.これは計算の順番だけのことではあるが,特に
Sarrusの方法と呼ばれている.
「右下がりは足し,左下がりは引く」感じは $2$ 次の場合と同じ雰囲気をもっている.しかし,$4$ 次以上になるとそのような見方はできなくなる.
$\left(\begin{array}{ccc}a&0&0\\ *&b&0\\ *& *&c\end{array}\right)$
または
$\left(\begin{array}{ccc}a&*&*\\ 0&b&*\\ 0&0&c\end{array}\right)$ の形の行列を
三角行列という.三角行列の行列式は
$\left|\begin{array}{ccc}a&0&0\\ *&b&0\\ *& *&c\end{array}\right|
=\left|\begin{array}{ccc}a&*&*\\ 0&b&*\\ 0&0&c\end{array}\right|
=abc$
と,簡単に計算できる.
$4$ 次以上の行列式については後述するが,一般に,正方行列 $A$ の行列式が $\det{A}$,$|A|$ などと表されることは $2$ 次の場合と同様である.