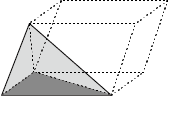
第7講 行列式の性質
3次の行列式と体積
$2$ 次の行列式が $xy$ 平面における平行四辺形の面積を表したように，
$3$ 次の行列式は $xyz$ 空間における平行六面体の体積を表す．
すなわち
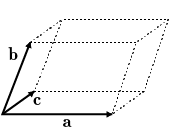のように，ベクトル $\mathbf{a}$，$\mathbf{b}$，$\mathbf{c}$ によってつくられる平行六面体の体積を $V$ とすると
$V=\big|\,\det(\ \mathbf{a}\ \mathbf{b}\ \mathbf{c}\ )\,\big|$
が成り立つ．
特に，$xyz$ 空間の四点 $\mathrm{A}$，$\mathrm{B}$，$\mathrm{C}$，$\mathrm{D}$ を頂点とする四面体の体積は $\det\big(\ \overrightarrow{\mathrm{AB}}\ \ \overrightarrow{\mathrm{AC}}\ \ \overrightarrow{\mathrm{AD}}\ \big)$ の絶対値の $1/6$ に等しいなぜ1/6？．
行列式の性質
二次の行列式について既に見た各性質は，一般の正方行列について成り立つ：
- 行と列を入れ替えても行列式の値は変わらない
- 列と列，あるいは行と行を入れ替えると符号が変わる
- 同じ列(行)を持つ行列の行列式は $0$
- 各行，各列について線型
-
ある列を何倍かして他の列に加えても行列式の値は変わらない
- ある行を何倍かして他の行に加えても行列式の値は変わらない
積の行列式
一般の正方行列 $A$，$B$ についても，やはり
$\det{(AB)}=\det{A}\det{B}$
が成り立つ．
$2$ 次の場合で見た通り，このことから導かれる重要な事実はいくつもあるが，
ここでは特に，$3$ 次の場合に成り立つ次のことに注意しておこう：
- $A$ を実 $3$ 次正方行列とし， ベクトル $\mathbf{a}_1$，$\mathbf{a}_2$，$\mathbf{a}_3$ がつくる平行六面体の体積を $V$ をとすると， ベクトル $A\mathbf{a}_1$，$A\mathbf{a}_2$，$A\mathbf{a}_3$ がつくる平行六面体の体積は $|\det{A}|V$ である なぜ？．
Cramerの公式
Cramerの公式も一般の次数で成り立つ．
すなわち，$n$ 次正方行列 $A=(\ \mathbf{a}_1\ \ \mathbf{a}_2\ \cdots\ \mathbf{a}_n\ )$ を係数行列とする連立一次方程式
$A\mathbf{x}=\mathbf{b}$
の解は，$\det{A}\neq0$ ならば
$
x_i=\dfrac{1}{\det{A}}\Big|\ \mathbf{a}_1\ \cdots\ \mathbf{a}_{i-1}\ \mathbf{b}\ \mathbf{a}_{i+1}\ \cdots\ \mathbf{a}_n\ \Big|\\[1mm]
\hspace{110pt}(i=1,2,\ldots,n)
$
により与えられる．$2$ 次の場合と同じく，線型性等の行列式の性質により容易に示される．