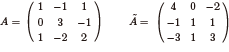第8講 余因子と逆行列
余因子
正方行列 $A=(a_{ij})$ の第 $i$ 行と第 $j$ 列を取り除いた行列を $A_{ij}$ と表すとき,$A$ の
$(i,j)$ 余因子 $\tilde{a}_{ij}$ は
$\tilde{a}_{ij}\stackrel{\mathrm{def}}{=}(-1)^{i+j}\det{A_{ij}}$
により定義される.
余因子の計算は符号に特に注意しよう.$(1,1)$ 余因子(左上端)の符号はサイズによらず必ず $+$ なのでそこから交互に符号を変わる.
-
$3$ 次の場合は
$\left|\begin{array}{ccc}\oplus&\ominus&\oplus\\\ominus&\oplus&\ominus\\\oplus&\ominus&\oplus\end{array}\right|$
と見るとよい.
$3\times 3$ 行列
$(a_{ij})=\left(\begin{array}{ccc}1&5&-2\\-1&2&0\\0&-4&3\end{array}\right)$
の $9$ 個の余因子をすべて計算してみると
$(1,1)$ 余因子
$\tilde{a}_{11}=\left|\begin{array}{ccc}\oplus&*&*\\*&2&0\\*&-4&3\end{array}\right|
=\left|\begin{array}{cc}2&0\\-4&3\end{array}\right|=6$
$(1,2)$ 余因子
$\tilde{a}_{12}=\left|\begin{array}{ccc}*&\ominus&*\\-1&*&0\\0&*&3\end{array}\right|
=-\left|\begin{array}{cc}-1&0\\0&3\end{array}\right|=3$
$(1,3)$ 余因子
$\tilde{a}_{13}=\left|\begin{array}{ccc}*&*&\oplus\\-1&2&*\\0&-4&*\end{array}\right|
=\left|\begin{array}{cc}-1&2\\0&-4\end{array}\right|=4$
$(2,1)$ 余因子
$\tilde{a}_{21}=\left|\begin{array}{ccc}*&5&-2\\\ominus&*&*\\*&-4&3\end{array}\right|
=-\left|\begin{array}{cc}5&-2\\-4&3\end{array}\right|=-7$
$(2,2)$ 余因子
$\tilde{a}_{22}=\left|\begin{array}{ccc}1&*&-2\\*&\oplus&*\\0&*&3\end{array}\right|
=\left|\begin{array}{cc}1&-2\\0&3\end{array}\right|=3$
$(2,3)$ 余因子
$\tilde{a}_{23}=\left|\begin{array}{ccc}1&5&*\\*&*&\ominus\\0&-4&*\end{array}\right|
=-\left|\begin{array}{cc}1&5\\0&-4\end{array}\right|=4$
$(3,1)$ 余因子
$\tilde{a}_{31}=\left|\begin{array}{ccc}*&5&-2\\*&2&0\\\oplus&*&*\end{array}\right|
=\left|\begin{array}{cc}5&-2\\2&0\end{array}\right|=4$
$(3,2)$ 余因子
$\tilde{a}_{32}=\left|\begin{array}{ccc}1&*&-2\\-1&*&0\\*&\ominus&*\end{array}\right|
=-\left|\begin{array}{cc}1&-2\\-1&0\end{array}\right|=2$
$(3,3)$ 余因子
$\tilde{a}_{33}=\left|\begin{array}{ccc}1&5&*\\-1&2&*\\*&*&\oplus\end{array}\right|
=\left|\begin{array}{cc}1&5\\-1&2\end{array}\right|=7$
-
$4$ 次だと符号は
$\left|\begin{array}{cccc}\oplus&\ominus&\oplus&\ominus\\\ominus&\oplus&\ominus&\oplus\\\oplus&\ominus&\oplus&\ominus\\\ominus&\oplus&\ominus&\oplus\end{array}\right|$
となる.
$(b_{ij})=\left(\begin{array}{cccc}1&0&2&0\\0&3&0&1\\2&-1&5&1\\-1&1&0&1\end{array}\right)$ とすると
$(2,3)$ 余因子
$\tilde{b}_{23}=\left|\begin{array}{cccc}1&0&*&0\\*&*&\ominus&*\\2&-1&*&1\\-1&1&*&1\end{array}\right|
=-\left|\begin{array}{ccc}1&0&0\\2&-1&1\\-1&1&1\end{array}\right|=2$
$(4,2)$ 余因子
$\tilde{b}_{42}=\left|\begin{array}{cccc}1&*&2&0\\0&*&0&1\\2&*&5&1\\*&\oplus&*&*\end{array}\right|
=\left|\begin{array}{ccc}1&2&0\\0&0&1\\2&5&1\end{array}\right|=-1$
余因子行列と逆行列
余因子と行列式との間には
$a_{i1}\tilde{a}_{j1}+a_{i2}\tilde{a}_{j2}+\cdots+a_{in}\tilde{a}_{jn}
=\left\{\begin{array}{ll}\det{A}&\mbox{if $i=j$}\\ 0&\mbox{if $i\neq j$}\end{array}\right.$
$a_{1i}\tilde{a}_{1j}+a_{2i}\tilde{a}_{2j}+\cdots+a_{ni}\tilde{a}_{nj}
=\left\{\begin{array}{ll}\det{A}&\mbox{if $i=j$}\\ 0&\mbox{if $i\neq j$}\end{array}\right.$
という関係がある
証明pdf.
この関係を踏まえて,$n\times n$ 行列 $A=(a_{ij})$ の
余因子行列を $\tilde{A}={}^t(\tilde{a}_{ij})$ により定義する.すなわち
$A=\left(\begin{array}{cccc}a_{11}&a_{12}&\cdots&a_{1n}\\a_{21}&a_{22}&\cdots&a_{2n}\\\vdots&\vdots&\ddots&\vdots\\a_{n1}&a_{n2}&\cdots&a_{nn}\\\end{array}\right)$
ならば
$\tilde{A}=\left(\begin{array}{cccc}\tilde{a}_{11}&\tilde{a}_{21}&\cdots&\tilde{a}_{n1}\\\tilde{a}_{12}&\tilde{a}_{22}&\cdots&\tilde{a}_{n2}\\\vdots&\vdots&\ddots&\vdots\\\tilde{a}_{1n}&\tilde{a}_{2n}&\cdots&\tilde{a}_{nn}\\\end{array}\right)$
である.番号の付き方に特に注意しよう.余因子行列においては
$(i,j)$ 余因子 $\tilde{a}_{ij}$を $(j,i)$ の位置に配置するのである.
このように定義された余因子行列は
$A\tilde{A}=\tilde{A}A=(\det{A})E$
を満たすので,$\det{A}\neq0$ ならば $A$ の
逆行列 $A^{-1}$ が存在して
$A^{-1}=\dfrac{1}{\det{A}}\tilde{A}$
となる.
一般の正方行列の逆行列の定義はもちろん $2$ 次の場合と同様である.
すなわち,実 $n$ 次正方行列 $A$ の
逆行列 $A^{-1}$ とは
$AA^{-1}=A^{-1}A=E$
を満たすものをいう.ここで,$E$ は $n$ 次の単位行列
$E=\left(\begin{array}{cccc}1&0&\cdots&0\\0&1&\cdots&0\\ \vdots&\vdots&\ddots&\vdots\\0&0&\cdots&1\\\end{array}\right)$
である.逆行列をもつ( $\det{A}\neq0$ となる) ような行列を
正則行列という.
また,一般の正方行列 $A$,$B$ についても
$\det{(AB)}=\det{A}\det{B}$
が成り立つのであったから
$A$ が正則ならば $\det{A^{-1}}=\dfrac{1}{\det{A}}$
$AB$ が正則 $\Leftrightarrow$ $A$,$B$ はともに正則
なども $2$ 次の場合と同様に成り立つ.
-
$A=\left(\begin{array}{ccc}1&-1&1\\0&3&-1\\1&-2&2\end{array}\right)$
の余因子行列を計算すると
$\tilde{A}=\left(\begin{array}{ccc}4&0&-2\\-1&1&1\\-3&1&3\end{array}\right)$
となる詳しく!.
$9$ 個の余因子は
$\tilde{a}_{11}=\left|\begin{array}{ccc}\oplus&*&*\\*&3&-1\\*&-2&2\end{array}\right|=\left|\begin{array}{cc}3&-1\\-2&2\end{array}\right|=4$
$\tilde{a}_{12}=\left|\begin{array}{ccc}*&\ominus&*\\0&*&-1\\1&*&2\end{array}\right|=-\left|\begin{array}{cc}0&-1\\1&2\end{array}\right|=-1$
$\tilde{a}_{13}=\left|\begin{array}{ccc}*&*&\oplus\\0&3&*\\1&-2&*\end{array}\right|=\left|\begin{array}{cc}0&3\\1&-2\end{array}\right|=-3$
$\tilde{a}_{21}=\left|\begin{array}{ccc}*&-1&1\\\ominus&*&*\\*&-2&2\end{array}\right|=-\left|\begin{array}{cc}-1&1\\-2&2\end{array}\right|=0$
$\tilde{a}_{22}=\left|\begin{array}{ccc}1&*&1\\*&\oplus&*\\1&*&2\end{array}\right|=\left|\begin{array}{cc}1&1\\1&2\end{array}\right|=1$
$\tilde{a}_{23}=\left|\begin{array}{ccc}1&-1&*\\*&*&\ominus\\1&-2&*\end{array}\right|=-\left|\begin{array}{cc}1&-1\\1&-2\end{array}\right|=1$
$\tilde{a}_{31}=\left|\begin{array}{ccc}*&-1&1\\*&3&-1\\\oplus&*&*\end{array}\right|=\left|\begin{array}{cc}-1&1\\3&-1\end{array}\right|=-2$
$\tilde{a}_{32}=\left|\begin{array}{ccc}1&*&1\\0&*&-1\\*&\ominus&*\end{array}\right|=-\left|\begin{array}{cc}1&1\\0&-1\end{array}\right|=1$
$\tilde{a}_{33}=\left|\begin{array}{ccc}1&-1&*\\0&3&*\\*&*&\oplus\end{array}\right|=\left|\begin{array}{cc}1&-1\\0&3\end{array}\right|=3$
となるので,各余因子の配置場所に注意して
$\tilde{A}={}^t\left(\begin{array}{ccc}4&-1&-3\\0&1&1\\-2&1&3\end{array}\right)
=\left(\begin{array}{ccc}4&0&-2\\-1&1&1\\-3&1&3\end{array}\right)$
が得られる.
$A\tilde{A}=\tilde{A}A=\left(\begin{array}{ccc}2&0&0\\0&2&0\\0&0&2\end{array}\right)$
となることがわかるので,$\det{A}=2$ であり,$A$ の逆行列
$A^{-1}=\dfrac{1}{2}\left(\begin{array}{ccc}4&0&-2\\-1&1&1\\-3&1&3\end{array}\right)$
が得られる.
-
余因子行列を求めるのはあまり楽な計算ではないが,
少なくとも $3\times 3$ 行列で数字が大きくない場合の逆行列を手早く計算するには良い方法なので,しっかり練習しておきたい.
慣れればある程度暗算でシンプルに求められるようになると思う:
-
$B=\left(\begin{array}{ccc}1&-2&3\\1&0&1\\3&1&2\end{array}\right)$
の余因子行列を同様にして求めると
$\tilde{B}=\left(\begin{array}{ccc}-1&7&-2\\1&-7&2\\1&-7&2\end{array}\right)$
となり,この場合は
$B\tilde{B}=\tilde{B}B=O$ (零行列)
となるので,$\det{B}=0$,従って $B$ は逆行列をもたない.
行列式の余因子展開
前節で見たように,余因子と行列式との間には
$\det{A}=a_{i1}\tilde{a}_{i1}+a_{i2}\tilde{a}_{i2}+\cdots+a_{in}\tilde{a}_{in}\\[1mm]
\hspace{23pt}=a_{1j}\tilde{a}_{1j}+a_{2j}\tilde{a}_{2j}+\cdots+a_{nj}\tilde{a}_{nj}$
という関係がある.行列式をこのように計算することを,それぞれ第 $i$ 行,第 $j$ 列に関する
余因子展開という.
行列式の計算は,前講までの方法ですべての場合に対応できるが,
余因子展開という見方をすると,より柔軟な計算が可能になる.
行列式 $\left|\begin{array}{ccc}1&2&3\\0&1&2\\3&1&1\end{array}\right|$
を余因子展開を用いて計算しよう.
任意の行,列で展開できるが,例えば第 $1$ 行で展開するならば
$\det{A}=a_{11}\tilde{a}_{11}+a_{12}\tilde{a}_{12}+a_{13}\tilde{a}_{13}$
と計算する.やはり余因子の符号に注意して(対応する余因子の符号を右肩に記す)
$\left|\begin{array}{ccc}1&2&3\\0&1&2\\3&1&1\end{array}\right|
=\left|\begin{array}{ccc}1^\oplus&*&*\\*&1&2\\*&1&1\end{array}\right|
+\left|\begin{array}{ccc}*&2^\ominus&*\\0&*&2\\3&*&1\end{array}\right|
+\left|\begin{array}{ccc}*&*&3^\oplus\\0&1&*\\3&1&*\end{array}\right|\\[1mm]
\hspace{43pt}
=1\cdot\left|\begin{array}{cc}1&2\\1&1\end{array}\right|
-2\cdot\left|\begin{array}{cc}0&2\\3&1\end{array}\right|
+3\cdot\left|\begin{array}{cc}0&1\\3&1\end{array}\right|\\[1mm]
\hspace{43pt}
=-1-(-12)+(-9)=2$
となる.
他の行や列でもやってみると
第 $2$ 行で展開:
$\left|\begin{array}{ccc}1&2&3\\0&1&2\\3&1&1\end{array}\right|
=\left|\begin{array}{ccc}*&2&3\\0^\ominus&*&*\\*&1&1\end{array}\right|
+\left|\begin{array}{ccc}1&*&3\\*&1^\oplus&*\\3&*&1\end{array}\right|
+\left|\begin{array}{ccc}1&2&*\\*&*&2^\ominus\\3&1&*\end{array}\right|\\[1mm]
\hspace{43pt}
=-0\cdot\left|\begin{array}{cc}2&3\\1&1\end{array}\right|
+1\cdot\left|\begin{array}{cc}1&3\\3&1\end{array}\right|
-2\cdot\left|\begin{array}{cc}1&2\\3&1\end{array}\right|\\[1mm]
\hspace{43pt}
=0+(-8)-(-10)=2$
第 $3$ 列で展開:
$\left|\begin{array}{ccc}1&2&3\\0&1&2\\3&1&1\end{array}\right|
=\left|\begin{array}{ccc}*&*&3^\oplus\\0&1&*\\3&1&*\end{array}\right|
+\left|\begin{array}{ccc}1&2&*\\*&*&2^\ominus\\3&1&*\end{array}\right|
+\left|\begin{array}{ccc}1&2&*\\0&1&*\\*&*&1^\oplus\end{array}\right|\\[1mm]
\hspace{43pt}
=3\cdot\left|\begin{array}{cc}0&1\\3&1\end{array}\right|
-2\cdot\left|\begin{array}{cc}1&2\\3&1\end{array}\right|
+1\cdot\left|\begin{array}{cc}1&2\\0&1\end{array}\right|\\[1mm]
\hspace{43pt}
=-9-(-10)+1=2$
などと計算できる.
もちろん行列式の性質
ある列(行)を何倍かして他の列(行)に加えても行列式の値は変わらない
ということを利用して,適切な形に変形してから余因子展開を用いるのがよい.
前講で見た「第 $1$ 行または第 $1$ 列の $(1,1)$ 成分以外をすべて $0$ にする」という基本方針は,実は余因子展開を利用する特別な場合なのであった.
行列式の性質および余因子展開を利用すると
$\left|\begin{array}{ccc}2&1&2\\5&1&7\\-2&-2&2\end{array}\right|
=\left|\begin{array}{ccc}0&1^\ominus&0\\3&1&5\\2&-2&6\end{array}\right|\qquad
\begin{array}{l}[\,\mathrm{c_2\stackrel{\times (-2)}{\to} c_1}\,]\\ [\,\mathrm{c_2\stackrel{\times (-2)}{\to} c_3}\,]\end{array}\\
\hspace{59pt}=-1\cdot\left|\begin{array}{cc}3&5\\2&6\end{array}\right|\qquad[\,\mbox{第 $1$ 行で展開}\,]\\
\hspace{59pt}=-8$
あるいは
$\left|\begin{array}{ccc}2&1&2\\5&1&7\\-2&-2&2\end{array}\right|
=\left|\begin{array}{ccc}-3&0&-5\\5&1^\oplus&7\\8&0&16\end{array}\right|\qquad
\begin{array}{l}[\,\mathrm{r_2\stackrel{\times (-1)}{\to} r_1}\,]\\ [\,\mathrm{r_2\stackrel{\times 2}{\to} r_3}\,]\end{array}\\
\hspace{59pt}=1\cdot\left|\begin{array}{cc}-3&-5\\8&16\end{array}\right|\qquad[\,\mbox{第 $2$ 列で展開}\,]\\
\hspace{59pt}=-8$
などと計算できる.