第19講 最小二乗法
直交射影と最短距離
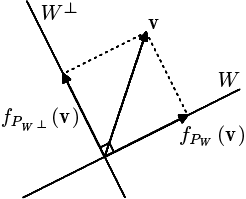
$(V,(\cdot,\cdot))$ を内積空間とし,$W$ を $V$ の部分空間,$W^\bot$ をその直交補空間とるするとき,任意の $\mathbf{v}\in V$ は
$\mathbf{v}=\mathbf{w}+\mathbf{w}^\bot\quad(\mathbf{w}\in W,\ \mathbf{w}^\bot\in W^\bot)$
と一意的に表され,$\mathbf{v}$ にこの $\mathbf{w}$ を対応させる線型写像を $V$ から $W$ への直交射影といい,$f_{P_W}$ と表わすのであった(
第18講).
$W^\bot$ も部分空間であるから,$V$ から $W^\bot$ への直交射影 $f_{P_{W^\bot}}$ も同じく定義され
$\mathbf{v}=f_{P_W}(\mathbf{v})+f_{P_{W^\bot}}(\mathbf{v})\quad(\mathbf{v}\in V)$
が成り立つ.
ところで,内積空間においては
$\|\mathbf{v}\|=\sqrt{(\mathbf{v},\mathbf{v})}$
によりノルム $\|\cdot\|$ が自然に定義され(
第13講),
$\|\mathbf{v}-\mathbf{w}\|$ は二つのベクトル $\mathbf{v}$ と $\mathbf{w}$ との「距離(近さ)」を表すと考えられるから,この意味で,$f_{P_W}(\mathbf{v})$ は $W$ のベクトルの中で $\mathbf{v}$ に最も「近い」ベクトルということができる.
さらに
$\|\mathbf{v}-f_{P_W}(\mathbf{v})\|=\|f_{P_{W^\bot}}(\mathbf{v})\|$
より,$\|f_{P_{W^\bot}}(\mathbf{v})\|$ はベクトル $\mathbf{v}$ から部分空間 $W$ への「最短距離」を与えることになる
詳しく!.
一般に,$\mathbf{v}_1\in W$,$\mathbf{v}_2\in W^\bot$ ならば
$\|\mathbf{v}_1+\mathbf{v}_2\|^2=(\mathbf{v}_1+\mathbf{v}_2,\mathbf{v}_1+\mathbf{v}_2)\\
\hspace{47pt}=(\mathbf{v}_1,\mathbf{v}_1)+(\mathbf{v}_1.\mathbf{v}_2)\\
\hspace{85pt}+(\mathbf{v}_2,\mathbf{v}_2)+(\mathbf{v}_2,\mathbf{v}_2)\\
\hspace{47pt}=(\mathbf{v}_1,\mathbf{v}_1)+(\mathbf{v}_2,\mathbf{v}_2)\\
\hspace{47pt}=\|\mathbf{v}_1\|^2+\|\mathbf{v}_2\|^2$
が成り立つから,$\mathbf{v}\in V$ が与えられたとき,$\mathbf{w}\in W$ ならば
$\|\mathbf{v}-\mathbf{w}\|^2
=\|f_{P_W}(\mathbf{v})-\mathbf{w}+f_{P_{W^\bot}}(\mathbf{v})\|^2\\
\hspace{41pt}=\|f_{P_W}(\mathbf{v})-\mathbf{w}\|^2+\|f_{P_{W^\bot}}(\mathbf{v})\|^2$
となる.よって,$\|\mathbf{v}-\mathbf{w}\|$ が最小となるのは $\mathbf{w}=f_{P_W}(\mathbf{v})$ のときであって,最小値(最短距離)は $\|f_{P_{W^\bot}}(\mathbf{v})\|$ であることがわかる.
一般に,集合 $X$ における
距離(距離関数)$d$ とは,写像 $d:X^2\to \mathbf{R}$ であって次の条件を満たすものをいう(
参考:距離空間)
:
| $\mathrm{(i)}$ | $d(x,x')\ge 0$ |
| $\mathrm{(ii)}$ | $d(x,x')= 0\iff x=x'$ |
| $\mathrm{(iii)}$ | $d(x,x')= d(x',x)$ |
| $\mathrm{(iv)}$ | $d(x,x'')\le d(x,x')+d(x',x'')$ |
ノルム空間 $(V.\|\cdot\|)$ においては
$d(\mathbf{v},\mathbf{v}'):=\|\mathbf{v}-\mathbf{v}'\|$
と定めると,これが $V$ における上記の意味での距離となることは容易に確かめられる.
例えば,$\mathbf{R}^2$,$\mathbf{R}^3$ における通常のEuclidノルムは「矢印の長さ」を表すのだから,$\|\mathbf{v}-\mathbf{v}'\|$ を二つのベクトル $\mathbf{v}$ と $\mathbf{v}'$ との間の「距離」とみなすことに違和感はないであろう.
実際,$\left(\begin{array}{c}x\\y\end{array}\right),\left(\begin{array}{c}x'\\y'\end{array}\right)\in\mathbf{R}^2$ に対して
$\left\|\left(\begin{array}{c}x\\y\end{array}\right)-\left(\begin{array}{c}x'\\y'\end{array}\right)\right\|
=\left\|\left(\begin{array}{c}x-x'\\y-y'\end{array}\right)\right\|\\
\hspace{72pt}=\sqrt{(x-x')^2+(y-y')^2}$
となり,これは通常の「二点間の距離」を与える式である.
-
$\mathbf{R}^3$ (内積はドット積)において
$W=\left\{\left.\,\left(\begin{array}{c}x\\y\\z\end{array}\right)\,\right|\,\dfrac{x}{2}=y=\dfrac{z}{3}\,\right\}\\
\mathbf{v}=\left(\begin{array}{c}4\\-1\\7\end{array}\right)$
とする.$W$ の正規直交基底は $\left\{\,\dfrac{1}{\sqrt{14}}\left(\begin{array}{c}2\\1\\3\end{array}\right)\,\right\}$ がとれるから,$W$ への直交射影を表す行列を $P_W$ とすると
$P_W\mathbf{v}
=\left(\begin{array}{c}\frac{2}{\sqrt{14}}\\\frac{1}{\sqrt{14}}\\\frac{3}{\sqrt{14}}\end{array}\right)\left(\begin{array}{ccc}\frac{2}{\sqrt{14}}&\frac{1}{\sqrt{14}}&\frac{3}{\sqrt{14}}\end{array}\right)
\left(\begin{array}{c}4\\-1\\7\end{array}\right)\\
\hspace{20pt}=
\dfrac{28}{\sqrt{14}}\left(\begin{array}{c}\frac{2}{\sqrt{14}}\\\frac{1}{\sqrt{14}}\\\frac{3}{\sqrt{14}}\end{array}\right)\\
\hspace{20pt}=
\left(\begin{array}{c}4\\2\\6\end{array}\right)$
$P_{W^\bot}\mathbf{v}
=\left(\begin{array}{c}4\\-1\\7\end{array}\right)-\left(\begin{array}{c}4\\2\\6\end{array}\right)=
\left(\begin{array}{c}0\\-3\\1\end{array}\right)$
となる.
よって,$\|\mathbf{v}-\mathbf{w}\|\quad (\mathbf{w}\in W)$ が最小となるのは
$\mathbf{w}=P_W\mathbf{v}
=\left(\begin{array}{c}4\\2\\6\end{array}\right)$
のときであって,最小値は
$\|P_{W^\bot}\mathbf{v}\|=\left\|\left(\begin{array}{c}0\\-3\\1\end{array}\right)\right\|
=\sqrt{10}$
である.
以上の計算を $xyz$ 空間における点とその位置ベクトルを同一視する観点からみると,点 $(4,-1,7)$ にもっとも近い直線 $\dfrac{x}{2}=y=\dfrac{z}{3}$ 上の点は $(4,2,6)$ であり,その最短距離は $\sqrt{10}$ ということになる.
-
$\mathbf{R}^3$ (内積はドット積)において
$W=\left\{\left.\,\left(\begin{array}{c}x\\y\\z\end{array}\right)\,\right|\,x-3y-5z=0\,\right\}\\
\mathbf{v}=\left(\begin{array}{c}1\\2\\6\end{array}\right)$
とする.$W$ の基底として $\left\{\,\left(\begin{array}{c}3\\1\\0\end{array}\right),\left(\begin{array}{c}5\\0\\1\end{array}\right)\,\right\}$ がとれ,これを正規直交化して $\left\{\,\dfrac{1}{\sqrt{10}}\left(\begin{array}{c}3\\1\\0\end{array}\right),\dfrac{1}{\sqrt{35}}\left(\begin{array}{c}1\\-3\\2\end{array}\right)\,\right\}$ が得られるから,$W$ への直交射影を表す行列を $P_W$ とすると
$P_W\mathbf{v}
=\left(\begin{array}{c}\frac{3}{\sqrt{10}}\\\frac{1}{\sqrt{10}}\\0\end{array}\right)\left(\begin{array}{ccc}\frac{3}{\sqrt{10}}&\frac{1}{\sqrt{10}}&0\end{array}\right)
\left(\begin{array}{c}1\\2\\6\end{array}\right)\\
\hspace{80pt}+\left(\begin{array}{c}\frac{1}{\sqrt{14}}\\-\frac{3}{\sqrt{14}}\\\frac{2}{\sqrt{14}}\end{array}\right)\left(\begin{array}{ccc}\frac{1}{\sqrt{14}}&-\frac{3}{\sqrt{14}}&\frac{2}{\sqrt{14}}\end{array}\right)
\left(\begin{array}{c}1\\2\\6\end{array}\right)\\
\hspace{20pt}=
\dfrac{1}{2}\left(\begin{array}{c}3\\1\\0\end{array}\right)
+\dfrac{1}{2}\left(\begin{array}{c}1\\-3\\2\end{array}\right)\\
\hspace{20pt}=
\left(\begin{array}{c}2\\-1\\1\end{array}\right)$
$P_{W^\bot}\mathbf{v}
=\left(\begin{array}{c}1\\2\\6\end{array}\right)-\left(\begin{array}{c}2\\-1\\1\end{array}\right)=
\left(\begin{array}{c}-1\\3\\5\end{array}\right)$
となる.
$W^\bot=\left\langle\,\left(\begin{array}{c}1\\-3\\-5\end{array}\right)\,\right\rangle=\left\{\left.\,\left(\begin{array}{c}x\\y\\z\end{array}\right)\,\right|\,x=-\dfrac{y}{3}=-\dfrac{z}{5}\,\right\}$
であって,$W^\bot$ の正規直交基底は $\left\{\,\dfrac{1}{\sqrt{35}}\left(\begin{array}{c}1\\-3\\-5\end{array}\right)\,\right\}$ がとれることが容易にわかるので,これから
$P_{W^\bot}\mathbf{v}
=\left(\begin{array}{c}\frac{1}{\sqrt{35}}\\-\frac{3}{\sqrt{35}}\\-\frac{5}{\sqrt{35}}\end{array}\right)\left(\begin{array}{ccc}\frac{1}{\sqrt{35}}&-\frac{3}{\sqrt{35}}&-\frac{5}{\sqrt{35}}\end{array}\right)
\left(\begin{array}{c}1\\2\\6\end{array}\right)\\
\hspace{20pt}=\left(\begin{array}{c}-1\\3\\5\end{array}\right)$
を先に求めてもよい.
よって,$\|\mathbf{v}-\mathbf{w}\|\quad (\mathbf{w}\in W)$ が最小となるのは
$\mathbf{w}=P_W\mathbf{v}
=\left(\begin{array}{c}2\\-1\\1\end{array}\right)$
のときであって,最小値は
$\|P_{W^\bot}\mathbf{v}\|=\left\|\left(\begin{array}{c}-1\\3\\5\end{array}\right)\right\|
=\sqrt{35}$
である.
以上の計算を $xyz$ 空間における点とその位置ベクトルを同一視する観点からみると,点 $(1,2,6)$ にもっとも近い平面 $x-3y-5z=0$ 上の点は $(2,-1,1)$ であり,その最短距離は $\sqrt{35}$ ということになる.
最小二乗法
実 $m\times n$ 行列 $A$ とベクトル $\mathbf{b}\in\mathbf{R}^n$ により
$A\mathbf{x}=\mathbf{b}$
と表わされる連立一次方程式を考えよう.
この連立一次方程式が解をもつための必要十分条件は $\mathbf{b}\in\mathrm{Im}f_A$ となることであった(
第17講).従って
$\mathbf{b}\notin\mathrm{Im}f_A$
ならば,この連立一次方程式は解をもたないのであるが,
次善の策として,$\mathbf{b}$ に最も「近い」$\mathrm{Im}f_A$ のベクトル
$\mathbf{b}'=P_{\mathrm{Im}f_A}\mathbf{b}$
により新しい連立一次方程式
$A\mathbf{x}=\mathbf{b}'$
を考えればこの方程式は解をもつ.これが
最小二乗法と呼ばれる方法であり,
こうして得られる解を
最小二乗解という.
ここで,$\mathbf{R}^n$ の内積はドット積(従ってノルムはEuclidノルム)を考えるのが普通である.そうでない一般の内積による議論は可能であるが,応用上の重要性は高くない.
$A\mathbf{x}=\mathbf{b}'$ を解いて最小二乗解 $\mathbf{x}_s$ が得られたとき
$\|A\mathbf{x}_s-\mathbf{b}\|=\|\mathbf{b}'-\mathbf{b}\|$
であり,$\mathbf{b}'$ の作り方からこれがベクトル $\mathbf{b}$ から部分空間 $\mathrm{Im}f_A$ への「最短距離」を与えていることがわかる.
$\mathbf{b}=\left(\begin{array}{c}b_1\\\vdots\\b_n\end{array}\right)$,$\mathbf{b}'=\left(\begin{array}{c}b'_1\\\vdots\\b'_n\end{array}\right)$ とすると,Euclidノルムは
$\displaystyle \|A\mathbf{x}_s-\mathbf{b}\|^2=|\mathbf{b}'-\mathbf{b}\|^2=\sum_{k=1}^n(b'_k-b_k)^2$
と計算されるので,$\mathbf{x}_s$ は「誤差の二乗和」を最小にするという意味で「最小二乗解」と呼ばれるのである.
-
連立一次方程式
$\left(\begin{array}{cc}1&2\\3&6\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}9\\7\end{array}\right)$
が解をもたないことは容易にわかる.そこで,$A=\left(\begin{array}{cc}1&2\\3&6\end{array}\right)$ とおき,$A$ が定める線型写像を $f_A$ とすると
$\mathrm{Im}f_A=\left\langle\,\left(\begin{array}{c}1\\3\end{array}\right),\left(\begin{array}{c}2\\6\end{array}\right)\,\right\rangle=\left\langle\,\left(\begin{array}{c}1\\3\end{array}\right)\,\right\rangle$
であって,$\mathrm{Im}f_A$ の正規直交基底は $\left\{\,\dfrac{1}{\sqrt{10}}\left(\begin{array}{c}1\\3\end{array}\right)\,\right\}$ がとれるから,$\mathrm{Im}f_A$ への直交射影を表す行列は
$P_{\mathrm{Im}f_A}=\dfrac{1}{10}\left(\begin{array}{c}1\\3\end{array}\right)\left(\begin{array}{cc}1&3\end{array}\right)$
となる.よって
$P_{\mathrm{Im}f_A}\left(\begin{array}{c}9\\7\end{array}\right)=\dfrac{1}{10}\left(\begin{array}{c}1\\3\end{array}\right)\left(\begin{array}{cc}1&3\end{array}\right)\left(\begin{array}{c}9\\7\end{array}\right)\\
\hspace{47pt}=\dfrac{30}{10}\left(\begin{array}{c}1\\3\end{array}\right)=\left(\begin{array}{c}3\\9\end{array}\right)$
より,新しい連立一次方程式
$\left(\begin{array}{cc}1&2\\3&6\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}3\\9\end{array}\right)$
は解をもち,実際 $x+2y=3$ で $y=t$ とおいて
$\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}3-2t\\t\end{array}\right)$
が得られる.これがもとの連立一次方程式の最小二乗解である.
-
連立一次方程式
$\left(\begin{array}{cc}1&2\\1&4\\1&3\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}2\\0\\4\end{array}\right)$
も解をもたない.実際,$A=\left(\begin{array}{cc}1&2\\1&4\\1&3\end{array}\right)$ とおき,$A$ が定める線型写像を $f_A$ とすると
$\mathrm{Im}f_A=\left\langle\,\left(\begin{array}{c}1\\1\\1\end{array}\right),\left(\begin{array}{c}2\\4\\3\end{array}\right)\,\right\rangle\\
\hspace{25pt}=\left\{\left.\,\left(\begin{array}{c}x\\y\\z\end{array}\right)\,\right|\,x+y-2z=0\,\right\}$
より $\left(\begin{array}{c}2\\0\\4\end{array}\right)\notin\mathrm{Im}f_A$ とわかる.
そこで,$\left\{\,\left(\begin{array}{c}1\\1\\1\end{array}\right),\left(\begin{array}{c}2\\4\\3\end{array}\right)\,\right\}$ は $\mathrm{Im}f_A$ の基底であり,これを正規直交化して $\left\{\,\dfrac{1}{\sqrt{3}}\left(\begin{array}{c}1\\1\\1\end{array}\right),\dfrac{1}{\sqrt{2}}\left(\begin{array}{c}-1\\1\\0\end{array}\right)\,\right\}$ が得られるから
$P_{\mathrm{Im}f_A}\left(\begin{array}{c}2\\0\\4\end{array}\right)=\dfrac{1}{3}\left(\begin{array}{c}1\\1\\1\end{array}\right)\left(\begin{array}{ccc}1&1&1\end{array}\right)\left(\begin{array}{c}2\\0\\4\end{array}\right)\\
\hspace{80pt}+\dfrac{1}{2}\left(\begin{array}{c}-1\\1\\0\end{array}\right)\left(\begin{array}{ccc}-1&1&0\end{array}\right)\left(\begin{array}{c}2\\0\\4\end{array}\right)\\
\hspace{47pt}=\dfrac{6}{3}\left(\begin{array}{c}1\\1\\1\end{array}\right)+\dfrac{-2}{2}\left(\begin{array}{c}-1\\1\\0\end{array}\right)=\left(\begin{array}{c}3\\1\\2\end{array}\right)$
より,新しい連立一次方程式
$\left(\begin{array}{cc}1&2\\1&4\\1&3\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}3\\1\\2\end{array}\right)$
を解いて
$\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}5\\-1\end{array}\right)$
が得られる.これがもとの連立一次方程式の最小二乗解である.
正規方程式
連立一次方程式 $A\mathbf{x}=\mathbf{b}$ の最小二乗解は
${}^t\!AA\mathbf{x}={}^t\!A\mathbf{b}$
を解いても得られる
証明.
$A$ が定める線型写像を $f_A$ とし,$W=\mathrm{Im}f_A$とおく.
$\mathbf{b}$ を
$\mathbf{b}=\mathbf{b}'+\mathbf{b}''\quad (\mathbf{b}'\in W,\ \mathbf{b}''\in W^\bot)$
と表すとき,$A\mathbf{x}=\mathbf{b}$ の最小二乗解とは,連立一次方程式 $A\mathbf{x}=\mathbf{b}'$ の解のことである.
また,$A=(\mathbf{a}_1\ \mathbf{a}_2\ \ldots\ \mathbf{a}_n)$とすると
$\mathrm{Im}f_A=\langle\mathbf{a}_1,\mathbf{a}_2,\ldots,\mathbf{a}_n\rangle$
であるから
$\mathbf{v}\in W^\bot\ \Leftrightarrow\ \mathbf{a}_1\cdot\mathbf{v}=\mathbf{a}_2\cdot\mathbf{v}=\cdots=\mathbf{a}_n\cdot\mathbf{v}=0\\
\hspace{38pt}\Leftrightarrow\ {}^t\!A\mathbf{v}=\mathbf{0}$
が成り立つ(
第18講).従って ${}^t\!A\mathbf{b}={}^t\!A\mathbf{b}'$ となることに注意しよう.
このことから,正規方程式 ${}^t\!AA\mathbf{x}={}^t\!A\mathbf{b}$ が必ず解をもつこともわかる.実際,$\mathbf{b}'\in W=\mathrm{Im}f_A$ より $\mathbf{b}'=A\mathbf{v}$ となるベクトル $\mathbf{v}$ が存在するから,${}^t\!A\mathbf{b}={}^t\!A\mathbf{b}'={}^t\!AA\mathbf{v}$ より,この $\mathbf{v}$ が解ということになる.
そこで,$\mathbf{x}_s$ を最小二乗解,すなわち $A\mathbf{x}_s=\mathbf{b}'$ が成り立つとすると
${}^t\!AA\mathbf{x}_s={}^t\!A\mathbf{b}'={}^t\!A\mathbf{b}$
が成り立つ.
逆に,${}^t\!AA\mathbf{x}_s={}^t\!A\mathbf{b}$ が成り立つとすると
${}^t\!A(A\mathbf{x}_s-\mathbf{b}')={}^t\!AA\mathbf{x}_s-{}^t\!A\mathbf{b}'={}^t\!AA\mathbf{x}_s-{}^t\!A\mathbf{b}=\mathbf{0}$
より $A\mathbf{x}_s-\mathbf{b}'\in W^\bot$ であるが,$W=\mathrm{Im}f_A$ だったから $A\mathbf{x}_s-\mathbf{b}'\in W$でもある.よって $A\mathbf{x}_s-\mathbf{b}'=\mathbf{0}$,すなわち $A\mathbf{x}_s=\mathbf{b}'$ が成り立つ.
この方程式は
正規方程式と呼ばれ,応用上はこれを利用することが多い.
前節の例で見た連立一次方程式の最小二乗解を,正規方程式を利用して求めよう.
-
連立一次方程式
$\left(\begin{array}{cc}1&2\\3&6\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}9\\7\end{array}\right)$
の正規方程式は
$\left(\begin{array}{cc}1&3\\2&6\end{array}\right)\left(\begin{array}{cc}1&2\\3&6\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{cc}1&3\\2&6\end{array}\right)\left(\begin{array}{c}9\\7\end{array}\right)$
すなわち
$\left(\begin{array}{cc}10&20\\20&40\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}30\\60\end{array}\right)$
であり,これを解いて
$\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}3-2t\\t\end{array}\right)\quad(t\in\mathbf{R})$
が得られる.
-
連立一次方程式
$\left(\begin{array}{cc}1&2\\1&4\\1&3\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}2\\0\\4\end{array}\right)$
の正規方程式は
$\left(\begin{array}{ccc}1&1&1\\2&4&3\end{array}\right)\left(\begin{array}{cc}1&2\\1&4\\1&3\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{ccc}1&1&1\\2&4&3\end{array}\right)\left(\begin{array}{c}2\\0\\4\end{array}\right)$
すなわち
$\left(\begin{array}{cc}3&9\\9&29\end{array}\right)\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}6\\16\end{array}\right)$
であり,これを解いて
$\left(\begin{array}{c}x\\y\end{array}\right)=\left(\begin{array}{c}5\\-1\end{array}\right)$
が得られる.
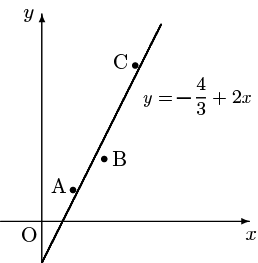
応用例として,次の問題を考える:
3点 $\mathrm{A}(1,1),\ \mathrm{B}(2,2),\ \mathrm{C}(3,5)$ を通る直線を求めよ
もちろんそんな直線はない.しかしともかく求める直線を $y=a_0+a_1x$ とおくと,満たすべき条件は
$a_0+a_1=1\\
a_0+2a_1=2\\
a_0+3a_1=5$
すなわち
$\left(\begin{array}{cc}1&1\\1&2\\1&3\end{array}\right)\left(\begin{array}{c}a_0\\a_1\end{array}\right)=\left(\begin{array}{c}1\\2\\5\end{array}\right)$
である.この連立一次方程式は解をもたないので,次善の策として最小二乗解を考える.正規方程式は
$\left(\begin{array}{ccc}1&1&1\\1&2&3\end{array}\right)\left(\begin{array}{cc}1&1\\1&2\\1&3\end{array}\right)\left(\begin{array}{c}a_0\\a_1\end{array}\right)=\left(\begin{array}{ccc}1&1&1\\1&2&3\end{array}\right)\left(\begin{array}{c}1\\2\\5\end{array}\right)$
から
$\left(\begin{array}{cc}3&6\\6&14\end{array}\right)\left(\begin{array}{c}a_0\\a_1\end{array}\right)=\left(\begin{array}{c}8\\20\end{array}\right)$
これを解いて $a_0=-\dfrac{4}{3},\ a_1=2$,従って
$y=-\dfrac{4}{3}+2x$
が得られる.この直線は与えられた3点のどれも通らないが
$(1,\frac{2}{3}),\ (2,\frac{8}{3}),\ (3,\frac{14}{3})$
とそれらの「近く」を通る直線である.この $y$ 座標の誤差の二乗和が最小という意味で,これは一つの最適解と言えるのである.